모든 확률변수는 확률분포를 가지며, 이 분포는 확률함수를 통해 정의된다.
(1) 결합분포 ( Joint Distribution )
- 결합분포(joint distribution)는 두 개 이상의 확률 변수에 대한 확률 분포를 말한다.
- 즉, 각각의 변수가 어떤 값을 가질 때 어떤 사건이 일어날 확률을 나타내는 함수이다.
- 예를 들어, X와 Y가 두 개의 확률 변수이고 (X,Y)로 표현한다면, 결합분포는 P(X=x,Y=y)로 표현된다.
- 이러한 결합분포는 각 변수의 확률분포를 알면 쉽게 구할 수 있다.
- 결합분포는 두 변수 간의 상관 관계를 분석하는 데 사용된다.
▶ 이산확률변수 & 결합확률질량함수
- 결합확률질량함수(joint probability mass function)는 이산형 확률변수들에 대해 사용되며, 각각의 확률변수가 가질 수 있는 값의 조합에 대한 확률값을 나타낸다.
- 두 이산 확률변수 X와 Y에 대한 결합확률질량함수는 아래와 같이 표현한다.

- n개의 이산 확률 변수에 대해서는 아래와 같이 표현한다.

◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 앞면과 뒷면의 수의 차이는 Y라는 확률변수라 했을 때, 확률변수 Y는 1,3 의 값을 갖는다.

- 이것을 표로 나타내면,

- 이 때 결합확률질량함수의 특징은 0과1 사이의 값을 갖는다. 그리고 함수의 합은 1이다.

▶ 연속확률변수 & 결합확률밀도함수
- 결합확률밀도함수(joint probability density function)는 연속형 확률변수들에 대해 사용되며, 결합확률밀도함수값이 두 변수의 구간에서 적분한 값은 해당 구간에서의 결합확률을 나타낸다.
- 두 연속 확률변수 X와 Y에 대한 결합확률밀도함수 f(x,y) 는 x,y에서의 밀도(높이)를 나타내며 아래의 성질을 만족한다.

- 밀도는 음수를 나타낼 수 없기 때문에 0보다 크거나 같다.
◈ 예제 : (X,Y) ~ U((0,u),(0,v))
- 균일분포의 결합확률밀도함수는,

- 이것을 그림으로 표현하면

(2) 주변분포(marginal distribution)
- 주변분포란 그 부분 집합에 속한 확률 변수들의 확률 분포를 뜻한다.
- 이는 다른 확률 변수의 값을 무시한 부분 집합 속의 확률 변수의 분포를 알 수 있게 해준다. 이는 조건부 확률과 대비되는 부분이다.
- 결합확률분포에서 한 확률변수에 대한 확률분포를 구할 때 사용하는 것이 주변분포(marginal distribution)이다.
- 주변분포는 결합분포에서 원하는 하나의 확률변수를 선택하고, 나머지 확률변수에 대해서는 모든 가능한 값들의 합 또는 적분을 통해 구할 수 있습니다. 이렇게 구해진 확률분포는 선택된 확률변수 하나에 대한 확률분포다.
- 예를 들어, (X, Y)의 결합분포가 주어졌을 때, X에 대한 주변분포를 구하고 싶다면, 모든 가능한 Y값에 대한 확률을 더하거나 적분하여 X의 분포를 구할 수 있다. Y에 대한 주변분포도 마찬가지로 모든 가능한 X값에 대한 확률을 더하거나 적분하여 구할 수 있다.
- 주변분포는 결합분포에서 원하는 확률변수에 대한 정보를 얻기 위해 사용되며, 다변량 확률론에서 중요한 개념 중 하나이다.
▶ 이산확률변수 & 주변확률질량함수(marginal probability mass function)
- 주변확률질량함수란, 결합확률질량함수에서 하나의 확률변수에 대한 확률분포를 구할 때 사용하는 확률함수입니다.
- 분할 (Partition) 이란 합쳐서 전체를 포괄하되(collectively exhaustive) 겹쳐서 전혀 중복이 안 되는 (mutually exclusive) 사건들의 집합을 말한다.
2023.04.24 - [통계학 공부] - 14. 조건부 확률 - 베이즈 정리 (Bayes' theorem)
14. 조건부 확률 - 베이즈 정리 (Bayes' theorem)
(1) 베이즈 정리 (Bayes' theorem) 베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리이다. 즉, 원인과 결과 형태의 문제에서 결과에 대한 원인 분석이 가능하게 하는
pmxsg.tistory.com
- 분할을 통해서 주변확률질량함수를 유도하면,

- 따라서, P(X=x) 를 구하는 식은,

- Y=y에 대한 식은,


◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 앞면과 뒷면의 수의 차이는 Y라는 확률변수라 했을 때, 확률변수 Y는 1,3 의 값을 갖는다.
- 주변확률분포

- 주변확률질량함수
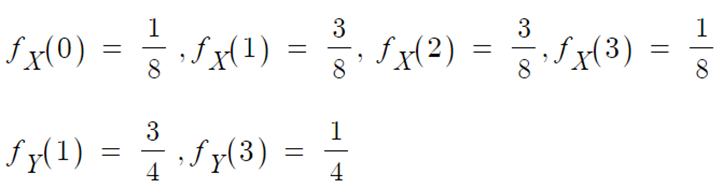
▶ 연속확률변수 & 주변확률밀도함수(marginal probability density function)
- 결합확률밀도함수를 통해 얻은 다변수 확률분포에서 한 변수의 확률분포를 구하는 것이 주변확률밀도함수입니다.

◈ 예제 : (X,Y) ~ U((0,u),(0,v))
- 균일분포의 주변확률밀도함수는,
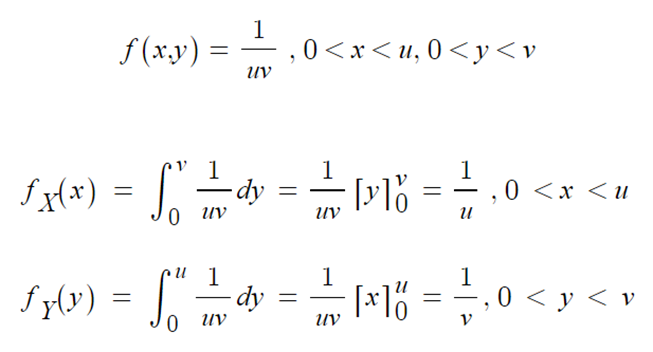
(3) 독립변수
- 독립확률변수란, 두 확률변수의 결합분포가 주변확률분포의 곱과 같아지는 확률변수를 의미한다. 즉, 하나의 확률변수가 다른 확률변수의 값을 예측하는 데 전혀 도움이 되지 않는 경우를 의미한다.
- 독립확률변수 X와 Y가 있다면, X가 어떤 값을 갖더라도 Y의 분포에는 영향을 미치지 않고, Y가 어떤 값을 갖더라도 X의 분포에는 영향을 미치지 않는다. 따라서, 두 변수의 공분산은 0이 되며, 독립성은 상관계수가 0이 되는 것으로 나타낼 수 있다.
- 독립확률변수는 다변량 확률분포와 조건부 확률 등의 개념에서 사용된다.
▶ 사건 A와 사건 B가 독립일 때,

▶ 두 확률변수 X와 Y는 독립이란 것은 모든 x, y에 대해 독립이라는 의미.
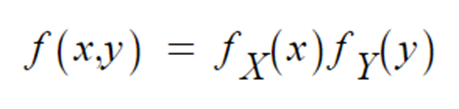
▶ n개의 확률변수 일 때,

◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 앞면과 뒷면의 수의 차이는 Y라는 확률변수라 했을 때, 확률변수 Y는 1,3 의 값을 갖는다.

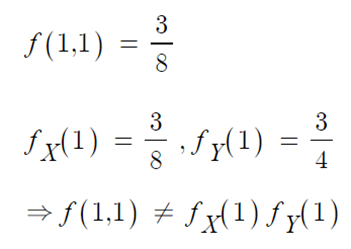
→ X와 Y는 독립이 아니다.
◈ 예제 : 독립인 경우

- 결합분포와 주변분포를 표로 나타내면,
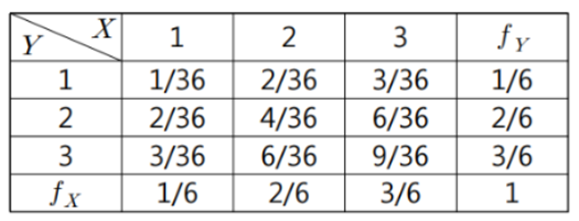
- 이 경우 모든 x, y에 대해,
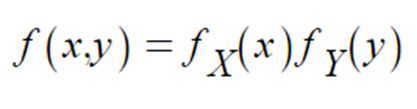
- 위 식이 성립함을 알 수 있다. 이 경우 X, Y는 독립이다.
'통계학 공부' 카테고리의 다른 글
| 22. 이산확률분포 - 베르누이 분포 & 이항분포 (0) | 2023.05.02 |
|---|---|
| 21. 확률변수의 공분산과 상관관계 (0) | 2023.05.01 |
| 19. 확률변수의 분산과 표준편차 (0) | 2023.04.29 |
| 18. 확률변수의 기대값 (Expected Value) (0) | 2023.04.28 |
| 17. 확률질량함수 & 확률밀도함수 (0) | 2023.04.27 |




댓글