(1) 베이즈 정리 (Bayes' theorem)
베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리이다.
즉, 원인과 결과 형태의 문제에서 결과에 대한 원인 분석이 가능하게 하는 이론인 것이다.

베이즈 정리를 이해하기 위해서 필요한 기본 이론이 있다.
(2) 확률의 기본정리
▶ 공리적 확률( Probability Axioms) :
- 너무 당연해서 증명이 필요없는 확률
- 1933년 콜모고로프(A.N.Kolmogorov, 1903-1987)
① 표본 공간의 전체 확률은 1 이다.

② 사건 A의 확률 ( P(A) )이 0보다 크거나 같고 1보다 작거나 같다. 즉 사건 A는 표본공간의 부분집합이다.
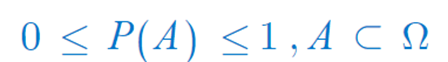
③ 서로 배반인 사건들의 합집합의 확률은 각각의 확률의 합과 같다.
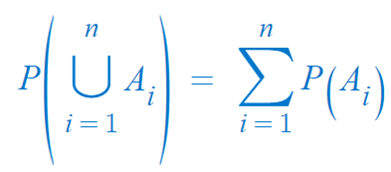
▶ 확률의 기본 정리





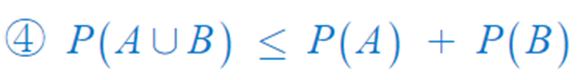
(3) 조건부 확률
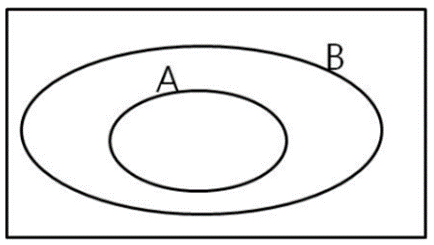
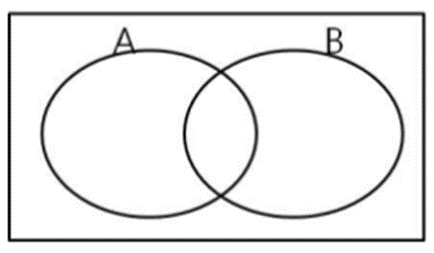
조건부 확률( conditional probability)이란 확률실험에서 새로운 정보 또는 조건(A)이 추가되었을 때, 사건 B의 확률을 말한다. 여기서 정보 또는 조건은 광범위한 표본 공간을 좁혀주는(narrow down) 역할을 한다.

사건 A가 발생했다면 A 이외의 것은 일어날 수 없다.
즉, A가 새로운 표본공간 Ω’ 이 되고, B가 발생한다는 것은 A와 B의 교집합에 있는 원소가 발생하는 것을 의미한다.
⇒ 사건 A가 주어졌을 때 사건 B의 조건부 확률을 식으로 표현하면,
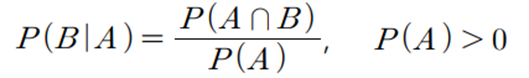
⇒ P(A | B) : 조건부 확률
- 사건 B가 주어진 조건 하에서 사건 A가 일어날 확률
- 사건 B에만 포커스를 맞춤
- 사건 B의 확률에 대한 사건 A와 B 결합사건 확률의 상대적 크기

(4) 분할 (partition)
합쳐서 전체를 포괄하되(collectively exhaustive) 겹쳐서 전혀 중복이 안 되는 (mutually exclusive) 사건들의 집합
예 ) 주사위를 한 번 던질 때 홀수가 나오는 사건과 짝수가 나오는 사건은 전체를 분할한다.
- 반례1) 홀수가 나오는 사건과 6이 나오는 사건(전체 포괄 못함)
- 반례2) 홀수가 나오는사건과 2 이상의 숫자가 나오는 사건(중복이 발생함)
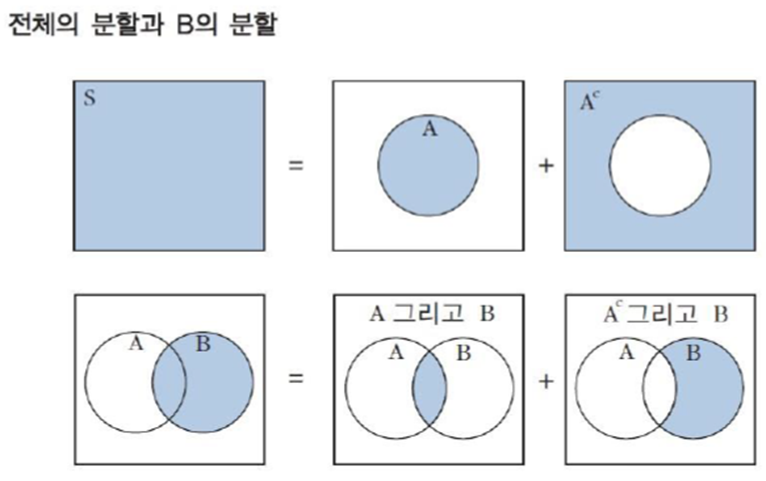
▶ 표본공간의 분할(partition) 을 식으로 표현하면,


(5) 독립
하나의 사건이 일어나느냐 마느냐 와 상관없이 다른 사건이 일어날 확률이 변하지 않으면, 두 사건의 관계가 독립(independent)이라고 한다. 그렇지 않은 경우 두 사건의 관계가 종속(dependent)이라고 한다.
복원추출일 경우에는 매번 추출이 독립이고, 비복원추출일 경우에는 종속이다.
두 사건이 서로 독립일 때, 두 사건이 모두 일어날 확률은 각각의 비조건부 확률을 곱하여 얻는다. 이를 좁은 의미의 곱셈법칙이라고 부른다.
두 사건 A와 B가 독립이면, P (A and B) = P(A) P(B)
독립사건을 식으로 표현하면,

A가 B에 영향을 안주고 B가 A에 영향을 주지 않는다면,

사건 A와 B가 서로 영향을 주고받지 않는 경우, "사건 A와 B는 독립사건이다"

표본공간과 공집합은 임의의 사건 A와 독립이다.

(6) 배반과 독립, 덧셈과 곱셈
▶ 상호배반 : 하나의 사건이 발생하면 다른 사건이 발행할 수 없는 경우
▶ 상호독립 : 하나의 사건이 발생하든 말든 다른 사건이 일어날 확률이 변하지 않는 경우
상호배반인 두 사건은 서로 종속이다. 두 사건 A,B가 상호배반이면 사건 A가 일어나는 경우 사건 B가 일어날 확률은 0으로 변경된다. 즉, 상호배반이면 독립일 수 없다.
▶ 덧셈법칙
- 두 사건 중 적어도 하나의 사건이 일어날 확률과 관련
- 좁은 의미의 덧셈법칙은 상호배반일 경우만 가능
- 배반이 아닌 경우 중복 계산되는 부분을 제거해야 한다.
▶ 곱셈법칙
- 두 사건이 함께 일어날 확률과 관련
- 좁은 의미의 곱셈법칙은 상호독립일 경우만 가능
- 독립이 아닌 (종속의) 경우 하나의 주변확률과 다른 하나의 조건부확률을 곱해야 한다.
(7) 사전확률&사후확률
사건 A가 주어졌을 때 사건 B의 조건부 확률

▶ 사전 확률 (prior probability)
- P(B | A) 은 순서적으로 볼 때, 대부분 사건 A가 먼저 발생하고 B가 이어 발생하는 상황에 대한 확률
- A는 원인, B는 결과의 형태를 가짐 ⇒ 코호트 연구 (Cohort Study)
- 전향적 연구(prospective study) : 원인 ⇒ 결과
- 원인의 가능성인 P(A) 또는 P(A)의 여사건은 사건 B가 관측되기 이전의 확률 ⇒ 사전확률 (prior probability)
사전 확률은 특정 사상이 일어나기 전의 확률을 뜻한다. 또는 경계 확률, 선험적 확률은 베이즈 추론에서 관측자가 관측을 하기 전에 가지고 있는 확률 분포를 의미한다. 사전 확률과 가능도가 주어졌을 때, 관측자는 관측값을 얻은 다음 베이즈 정리에 의해 사후 확률을 얻을 수 있다.
▶ 사후 확률 (posterior probability)
- 어떤 문제에서는 결과를 얻은 상태에서 그 결과가 발생하게 된 원인을 역으로 추정 ⇒ 사례-대조연구(case-control study)
- 후향적 연구(retrospective study) : 결과 ⇒ 원인
- 결과 B의 관측했을 때 그 원인이 A일 사건의 확률은 ? P(A | B)
- 사건 B가 관측된 후의 A의 확률 ⇒ 사후확률
사후 확률은 베이즈의 정리를 적용하여 가능성으로 요약된 정보로 사전 확률을 업데이트한 결과인 조건부 확률의 일종이다. 인식론적 관점에서 사후 확률은 사전 지식과 특정 시간에 사용 가능한 관찰을 설명하는 수학적 모델이 주어지면 불확실한 명제에 대해 알아야 할 모든 것을 포함한다.
◈ 예제 : 암진단
암 간이진단 검사를 실시하였다.
암에 걸렸을 때 양성반응이 나올 확률은 0.96
암에 걸리지 않았을 때 양성반응이 나올 확률이 0.05
☆ 만약 검사에서 양성반응이 나왔다면, 암에 걸렸을 확률은 ?
⇒ 확률적으로 표현해서 사건 A를 암에 걸린 사건으로 P(A)
사건 B를 양성반응인 사건으로 P(B) 로 설정했을 때, 위의 내용을 수식으로 하면

질문인 검사에서 양성반응이 나왔다면, 암에 걸렸을 확률을 수식으로 하면 P(A | B) 를 구하면 된다.

위의 식에서 알아야 할 부분은 암에 걸릴 확률(P(A)) 이다.
사전 정보가 필요하다. 즉 사전확률 P(A)를 0.001 이라고 가정한다.

계산 결과 약 1.9 % 의 확률이 나온다. 즉 양성반응이 나왔을 때 암에 걸렸을 확률이 1.9% 인 것이다.
이 수치는 기존 암에 걸릴 확률(사전 확률)인 0.001보다는 19배 높은 수치이지만, 암에 걸렸을 때 양성반응이 나올 확률은 0.96 이라는 수치를 보고서 예상했을 암에 걸릴 확률을 생각했던 것과 비교해 보면 현저히 낮은 수준일 것이다.
(8) 베이즈 정리의 본질
베이즈 정리의 본질은 “입장을 바꿔 생각” 함으로써 미지의 세계에 대해 추론하는 것이다.
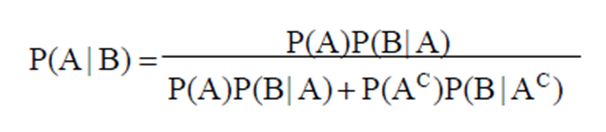
좌변의 조건부확률 P(A | B)를 구하기 위해 우변에 P(B | A), P(B|Ac) 등으로 “입장이 바뀐” 조건부확률이 이용되고 있다.
위의 암진단 예제에서 양성반응이 나왔을 때 암일 경우를 입장을 바꾸어 암이 걸렸을 때와 암이 걸리지 않았을 때 양성반응이 나오는 경우를 입장 바꿔 알아본 결과이다.
▶ 확률수형도 (probability tree)

▶ 베이즈 정리의 일반화
{A1, A2, ..., Am} = 표본공간(Ω)의 분할

P (B) > 0 일 때,
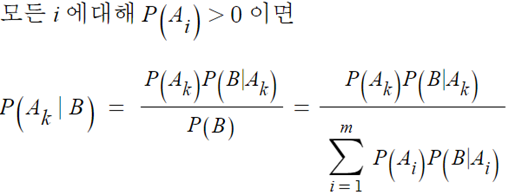
'통계학 공부' 카테고리의 다른 글
| 16. 확률변수와 확률분포 (0) | 2023.04.26 |
|---|---|
| 15. 조건부 확률 - 베이즈 정리 II (0) | 2023.04.25 |
| 13. 확률 - 경우의 수 (1) | 2023.04.23 |
| 12. 확률과 통계 (0) | 2023.04.22 |
| 11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 (0) | 2023.04.21 |




댓글