표본공간에 있는 원소의 형태에 따라 확률변수의 형태가 다르게 나올 수 있다.
표본공간의 원소가 셀 수 있는 수치자료라면 즉 이산자료라면 확률변수도 셀 수 있게 나오고, 연속적인 실수형태라면 확률변수도 실수형태로 나타날 수 있다.
▶ 이산확률변수(discrete random variable) :
확률변수가 가질 수 있는 값들이 가산(countable) 또는 셀 수 있는 경우
예) 불량품의 개수, 사고 건수,...
▶ 연속확률변수(continuous random variable) :
가질 수 있는 값이 셀 수 없을 정도로 많은 경우
예) 신장, 체중, ...
(1) 확률변수, 확률함수, 확률분포
- 확률변수: 특정 확률실험에서 발생 가능한 결과를 수치화하여 나타낸 변수를 의미한다. 즉, 확률실험에서 어떤 값을 취할 수 있는 변수를 의미한다,
- 확률함수: 확률변수가 가질 수 있는 모든 값에 대해 해당 값이 나올 확률을 나타내는 함수를 말한다. 이 함수는 주로 확률질량함수 또는 확률밀도함수로 나타내어진다.
- 확률분포: 확률변수가 가질 수 있는 모든 값에 대한 확률을 나타내는 분포를 의미한다. 이 분포는 주로 이산확률변수의 경우 확률질량함수로, 연속확률변수의 경우 확률밀도함수로 나타내어진다.
즉, 셋의 관계를 정리하면, "확률실험 내 모든 확률변수가 확률함수를 통하여 나오는 값들의 집합이 확률분포이다" 라고 표현할 수 있다.
확률분포는 확률변수의 가능한 값들과 그 값들이 나타날 확률을 모두 나열한 것을 의미한다. 이 때, 이산확률분포와 연속확률분포로 나뉜다.
확률함수는 확률변수의 값을 입력으로 받아, 해당 값이 나타날 확률을 출력하는 함수를 말한다. 이산확률변수에 대해서는 확률질량함수, 연속확률변수에 대해서는 확률밀도함수가 확률함수 역할을 한다.
따라서, 모든 확률변수는 확률분포를 가지며, 이 분포는 확률함수를 통해 정의된다.
(2) 확률질량함수(probability mass function, PMF)
- 확률 질량 함수는 이산 확률 변수에서 특정 값에 대한 확률을 나타내는 함수이다.
- 즉, 이산 확률 변수의 확률구조를 나타낸다.
▶ 이산확률변수(discrete random variable) :
- 확률변수가 가질 수 있는 값들이 가산(countable) 또는 셀 수 있는 경우
- 예) 불량품의 개수, 사고 건수,...
▶ 표현방법
- 확률변수 : P(X=1) (Probability의 P를 사용하는 듯)
- 확률질량함수 : f (1) ( function의 f를 사용하는 듯)
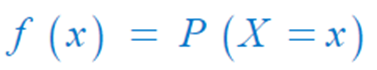
- 이산확률변수 X를 강조하기 위해 X를 추가하기도 함.

◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
각 확률변수의 값에 대한 확률은 아래와 같이 나타난다.

▶ 확률질량함수로 표현하면,

▶ 앞면과 뒷면의 수의 차이는 Y라는 확률변수라 했을 때, 확률변수 Y는 1,3 의 값을 갖는다.
이를 Y를 강조한 확률질량함수로 표현하면,
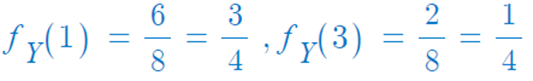
◈ 확률 질량 함수의 성질

⇒ 확률질량함수 역시 확률 이기 때문에 확률이 가지는 기본 성질을 똑같이 가진다.
확률의 기본정리 참조
1. 확률은 0과 1 사이이다.
2. 표본공간의 합은 1이다.
3. 임의의 구간에 있는 확률은 해당되는 구간 안의 모든 것을 더한 것이다.
▶ 누적분포함수 (cumulative distribution function, CDF)

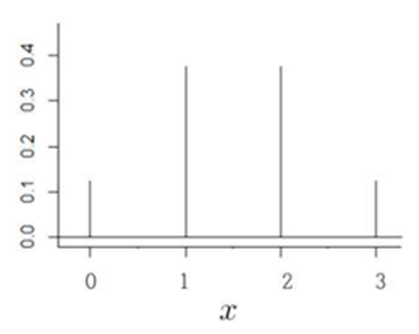
◈ 예제 : 동전 3개 던지기

▶ 질량함수를 그래프로 표현하면,
▶ 누적함수를 그래프로 표현하면,
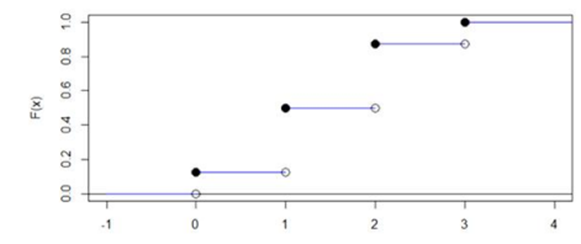
⇒ 점프 뛴 만큼이 그 지점에서의 확률
(3) 확률밀도함수(probability density function)
- 확률 밀도 함수는 연속 확률 변수의 분포를 나타내는 함수로 이산확률변수의 확률질량함수와 대응된다.
▶ 연속확률변수(continuous random variable) :
- 가질 수 있는 값이 셀 수 없을 정도로 많은 경우
- 예) 신장, 체중,..
▶ 히스토그램( Histogram )
- 히스토그램은 수치자료 특히 연속자료의 분포형태를 표시
- 계급의 상대도수를 사각형의 면적으로 표시 ⇒ 전체 면적 = 1
- 높이 = 상대도수 / 계급구간길이 = 밀도(density)표현 방법

⇒ 위의 그래프는 연속자료로 이루어진 모집단에서 표본 추출을 한 것이다.
각각 n = 100, 10,000, ∞ 를 일 때이다.
n = ∞ 이면 모집단이 된다. x일 때의 높이(=밀도) = f(x) : 확률밀도함수 가 된다.
◈ 예제 : 0~12까지의 숫자가 표시된 돌림판

- 그림과 같이 바늘이 지적하는 위치를 X 라 했을 때,
- 표본공간 Ω = { x : 0 〈 x ≤12 }
- 0에서 12까지 발생 가능성은 동일
- 즉, 밀도(=높이)는 이 구간에서 동일 : f(x) = c

- 전체 면적 = 1 이므로 f(x) = 1 / 12 , 0 〈 x ≤12
▶ 확률밀도함수에서의 확률
- 히스토그램의 면적 = 해당 구간에서의 비율(상대도수)
- 확률밀도함수의 면적 = 해당 구간에서의 확률
- 연속확률변수 X가 구간 [a , b]에 속할 확률은
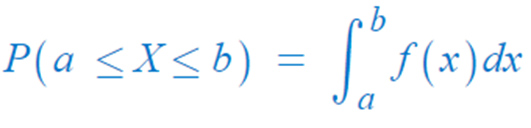
※ 면적을 구해야하기 때문에 적분(정의된 함수의 그래프와 그 구간으로 둘러싸인 도형의 넓이를 구하는 것)을 적용
▶ 확률밀도함수의 성질

▶ 누적분포함수 (cumulative distribution function, CDF)
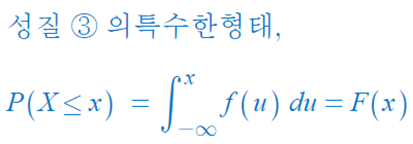
◈ 예제 : 0~12까지의 숫자가 표시된 돌림판
누적분포함수 F(x)의 값은,
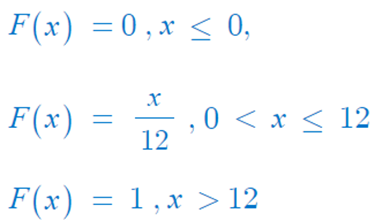
⇒ 연속된 선으로 연결되고 점프가 없다. 임의의 점에서의 확률은 0 ( 점은 면적이 아니기 때문이다. )
'통계학 공부' 카테고리의 다른 글
| 19. 확률변수의 분산과 표준편차 (0) | 2023.04.29 |
|---|---|
| 18. 확률변수의 기대값 (Expected Value) (0) | 2023.04.28 |
| 16. 확률변수와 확률분포 (0) | 2023.04.26 |
| 15. 조건부 확률 - 베이즈 정리 II (0) | 2023.04.25 |
| 14. 조건부 확률 - 베이즈 정리 (Bayes' theorem) (0) | 2023.04.24 |




댓글