(1) 확률변수 기대값의 정리
확률변수의 공분산을 구하기 위해서는 확률변수 기대값의 정리를 미리 파악해 둘 필요가 있다.
- E(X+Y) = E(X) + E(Y)
- X와 Y가 독립이면, E(XY) = E(X) E(Y)
2023.04.28 - [통계학 공부] - 18. 확률변수의 기대값 (Expected Value)
18. 확률변수의 기대값 (Expected Value)
확률변수의 통계량은 확률분포를 표현하기 위한 값들이며, 이 값들은 확률함수를 통해 계산할 수 있다. (1) 기대값 ( Expected Value) 확률변수에 대해 평균적으로 기대하는 값 = 모평균(population mean)
pmxsg.tistory.com
▶ 확률변수 X와 Y에 대해, X+Y의 기댓값? XY의 기댓값?
- 두 변수를 고려한다는 것은 일단 두 변수에 대한 결합분포가 있다는 것을 전제한다.
- 결합확률질량함수나 결합확률밀도함수를 이용한다.
- 각 확률변수의 기대값은,

2023.04.30 - [통계학 공부] - 20. 결합분포와 주변분포
20. 결합분포와 주변분포
모든 확률변수는 확률분포를 가지며, 이 분포는 확률함수를 통해 정의된다. (1) 결합분포 ( Joint Distribution ) 결합분포(joint distribution)는 두 개 이상의 확률 변수에 대한 확률 분포를 말한다. 즉, 각
pmxsg.tistory.com
▶ 이산확률변수
- E(X+Y) = E(X) + E(Y)

- 위와 같이 X+Y의 기대값을 결합확률질량함수로 표현할 수 있다.
- 이를 분리해서 다시 풀면 아래와 같다.

- X와 Y가 독립이면, E(XY) = E(X) E(Y)

- 위와 같이 XY의 기대값을 표현할 수 있다.
- 독립확률변수에서 위의 식은,

- 독립이면 위의 식이 성립한다. 따라서, 아래와 같이 정리할 수 있다.

(2) 확률변수의 공분산(Covariance)
- 공분산(covariance)은 두 변수 사이의 상관 관계를 나타내는 통계량이다.
- 두 변수 간에 얼마나 같이 변화하는지를 나타낸다.
- 확률변수의 공분산은 수치자료 표본공분산으로 부터 유도할 수 있다.
▶ 표본공분산
2023.04.21 - [통계학 공부] - 11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도
11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도
일변량 자료 요약 (1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등 (2) 범주형 - 도수분포표 (빈도수, 백분율) 다변량 자료 요약 (1) 수치형 - 공분산, 상관관계 (2) 범주형 - 분할표
pmxsg.tistory.com

- 위의 표본공분산 식을 아래와 같이 변형시키면,

- 위 식에 분모, 분자에 n을 곱하면,

▶ 확률변수 X와 Y의 공분산 : Cov(X,Y)
- 앞선 식에서 확률변수의 공분산을 유도하면,

- 이 식을 기대값의 정리를 기반으로 표현하면,

- 풀어서 정리하면,
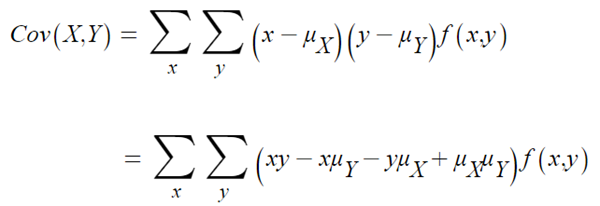
- 위 식을 각각 분리해서 보면,
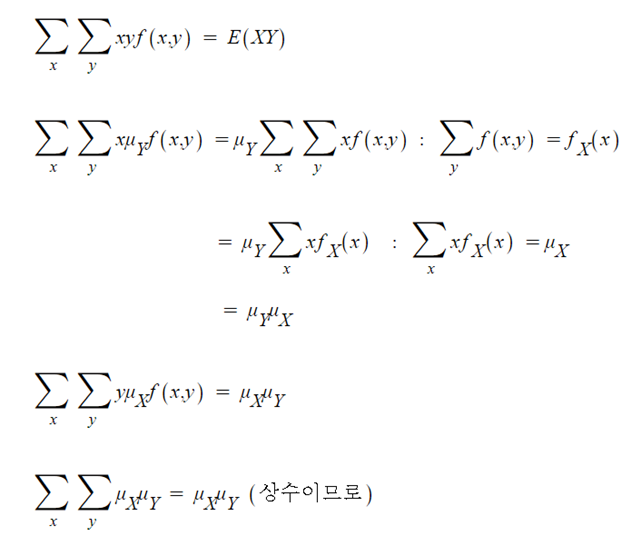
- 위에서 나온 값들을 식에 반영하면,
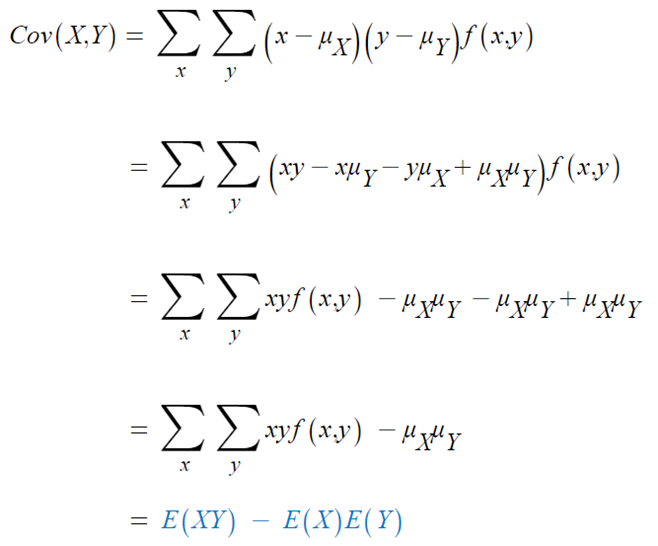
※ X와 Y가 독립이면, E(XY) = E(X) E(Y) 따라서 Cov(X,Y) = 0 이 된다.
역은 일반적으로 성립하지 않는다.
◈ 예제 : 아래의 결합확률분포표가 있다고 하면,
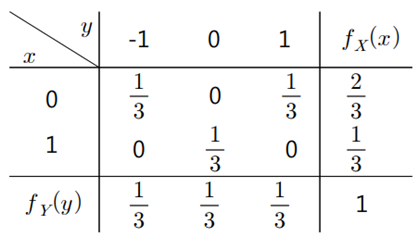
- 위 분포표의 공분산을 구하면,


- 위 분포표의 공분산은 0 이다.
▶ 공분산이 0이면 모든 E(XY)=E(X)E(Y) 인가 ?

⇒ 따라서 독립이 아니다. 역은 성립하지 않는다.
※ X와 Y가 독립이면, E(XY) = E(X) E(Y) 따라서 Cov(X,Y) = 0 이 된다.
역은 일반적으로 성립하지 않는다.
(3) 공분산의 성질
▶ 기대값의 성질
- 상수 a의 기대값 E(a) = a
- aX+b의 기대값 E(aX+b) = aE(X)+b
▶ 공분산의 성질
- Cov(aX+b, cY+d) = acCov(X,Y)
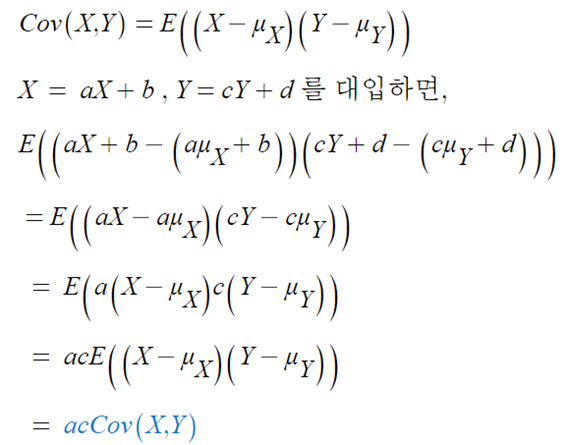
- Var(X±Y) = Var(X)+Var(Y) ± 2Cov(X,Y)
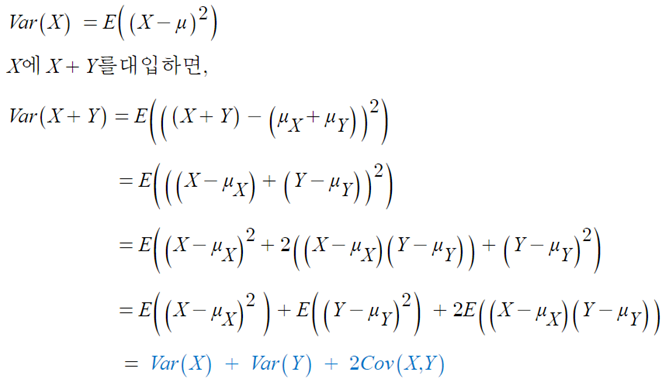
- X와 Y가 독립이면, Var(X±Y) = Var(X)+Var(Y)
※ X와 Y가 독립이면, E(XY) = E(X) E(Y), 따라서 Cov(X,Y) = 0 이 된다.
X와 Y가 독립이면, 공분산 Cov(X,Y)=0 이다. 따라서 , 위 공분산 성질은
Var(X±Y) = Var(X)+Var(Y) ± 2Cov(X,Y) ⇒ Var(X±Y) = Var(X)+Var(Y)
(4) 상관계수(coefficient of correlation)
- 공분산의 문제점은 측정단위에 영향을 받기 때문에 그 값 자체로는 선형관계의 정도를 알 수 없다.
- 따라서 표준화할 필요성이 있다.
- 상관계수는 표준화된 변수들의 공분산이다.
- 표준화 방법은, 변수에서 평균을 뺀 값을 표준편차로 나누어 새로운 표준화변수로 만든다.
▶ 표준화 변수들의 공분산
- 확률변수 X,Y를 표준화하면,
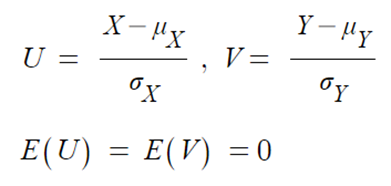
- 공분산 Cov(U,V) 는,
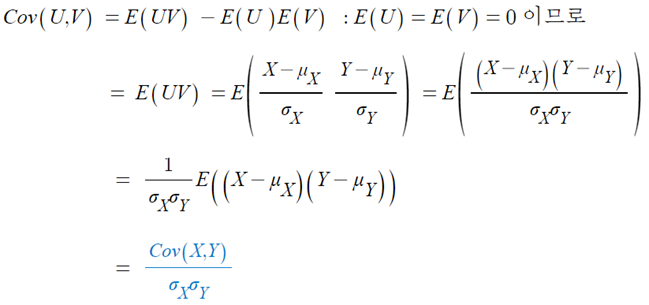
▶ 확률변수 X와 Y의 상관계수
- X와 Y의 상관계수는 표준화된 U,V의 공분산이다.
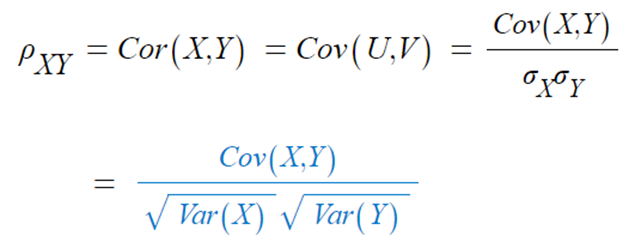
▶ 상관계수의 성질

※ 공분산과 상관계수 요약정리
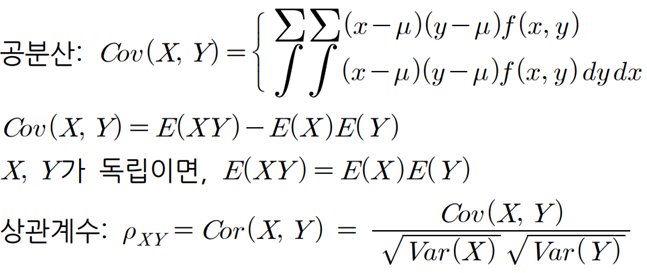
'통계학 공부' 카테고리의 다른 글
| 23. 이산확률분포 - 초기하분포(Hypergeometric Distribution) (0) | 2023.05.03 |
|---|---|
| 22. 이산확률분포 - 베르누이 분포 & 이항분포 (0) | 2023.05.02 |
| 20. 결합분포와 주변분포 (0) | 2023.04.30 |
| 19. 확률변수의 분산과 표준편차 (0) | 2023.04.29 |
| 18. 확률변수의 기대값 (Expected Value) (0) | 2023.04.28 |




댓글