일변량 자료에 대한 수치적 기술통계에서 표본들이 얼마나 퍼져있는지를 나타내는 대표적인 것이 표본분산과 표본 표준편차이다. 마찬가지로 확률변수에서도 분산과 표준편차를 확인해 볼 수 있다.
2023.04.18 - [통계학 공부] - 8. 수치자료의 산포 - 분산, 표준편차, 분위수
8. 수치자료의 산포 - 분산, 표준편차, 분위수
일변량 자료 요약 (1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등 (2) 범주형 - 도수분포표 (빈도수, 백분율) 다변량 자료 요약 (1) 수치형 - 공분산, 상관관계 (2) 범주형 - 분할표
pmxsg.tistory.com
(1) 수치자료의 표본분산
- 분산은 관측값에서 중심위치(평균)를 뺀 값을 제곱하고 그것을 모두 더한 값이다.
- 표본공간은 확률실험에서 나왔고 나온 원소들을 숫자로 바꿔 주는 것이 확률변수이다.
- 따라서 확률변수는 수치자료라 할 수 있다. 확률변수의 분산을 구할 때 일단 표본분산의 방법에서 시작한다.
- 표본분산은 아래와 같이 구할 수 있다.
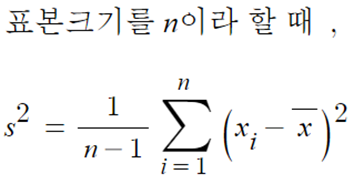
- 수치자료의 중심위치(평균)은 확률변수에서는 기대값으로 표현한다.
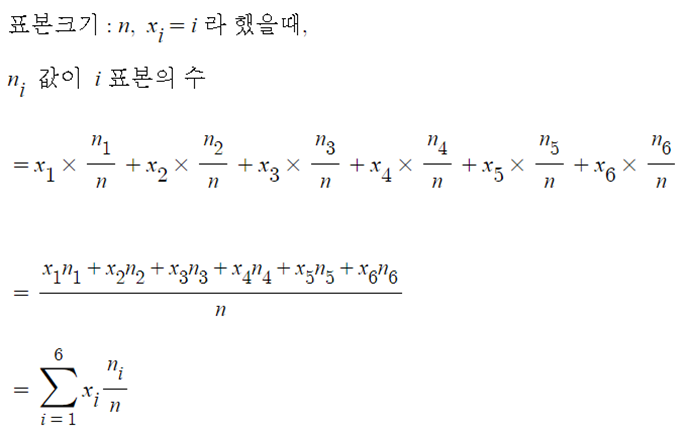
→ 표본평균에서 기대값으로 이끌어 낼 때의 방법이다.
따라서, 표본 분산은 아래와 같이 표현할 수 있다.

- 위 식에서 분자와 분모에 n을 각각 곱해주면,

(2) 모분산
2023.04.22 - [통계학 공부] - 12. 확률과 통계
12. 확률과 통계
(1) 확률과 통계 확률은 불확실성을 다루기 위한 수학적 도구이고, 통계는 데이터를 수집, 요약, 분석하여 패턴을 파악하는 학문이라 할 수 있다. 이러한 이유로 확률과 통계는 밀접한 관계를 가
pmxsg.tistory.com
- 확률은 알려진 모델이 주어져 있는 상황에서 data를 예측하는 것이다.
- 확률실험의 전제조건은 시행하기 전에 발생할 수 있는 모든 결과는 알 수 있어야 하고 실험을 하기 전까지 어떤 것이 발생할 것인지에 대해 확실하게 예측할 수 없어야 한다.
- 표본공간은 위의 식에서 표본크기라 할 수 있다.
- 위의 식에서 표본크기 n을 계속 크게한다면 마지막은 모집단이 될 것이다.
- 기대값을 구할 때 n을 크게 했을 때 모평균이 되었듯이, 위 표본 분산에서 n을 크게하면 모분산이 된다.
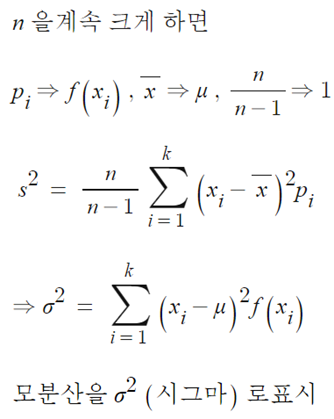
(3) 확률변수 X의 분산
- 확률변수 X의 분산을 Var(X)로 표시하면,
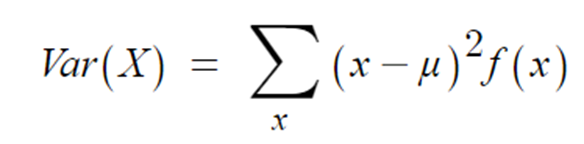
- 위 분산은 X에 어떤 변환된 함수의 기대값으로 볼 수 있다. 따라서, 아래와 같이 나타낼 수 있다.
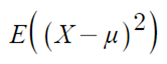
- 위 분산식을 풀어 정리하면,
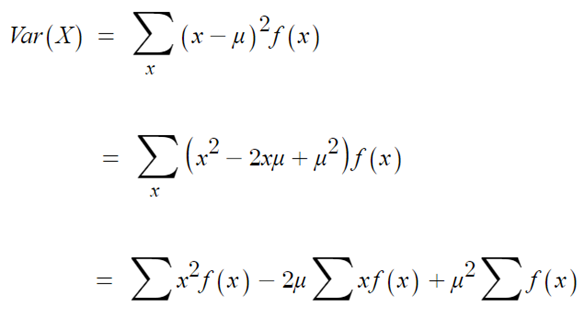
- 앞선 기대값을 구하는 식에서

- 위 식을 다시 기대값으로 표현하면,
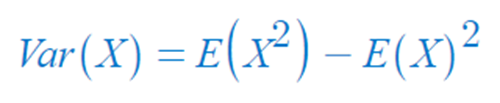
(4) 확률변수 X의 표준편차
- 표준편차는 분산의 제곱근이다.
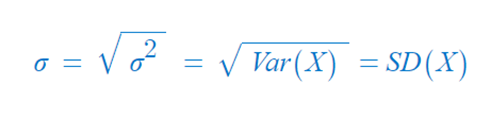
◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 각 확률변수의 값에 대한 확률은 아래와 같이 나타난다.
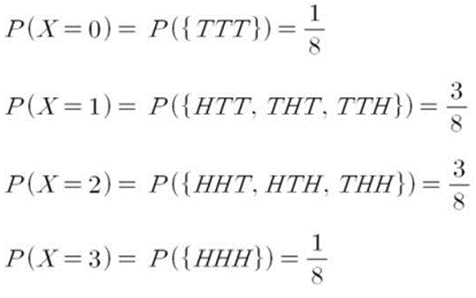
▶ 기대값 E(X)
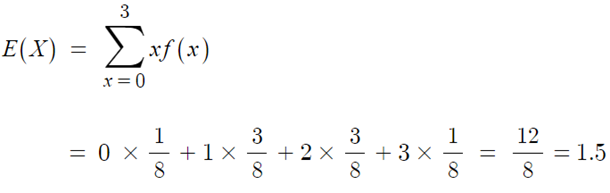
▶ 변형된 함수의 기대값 E(X)
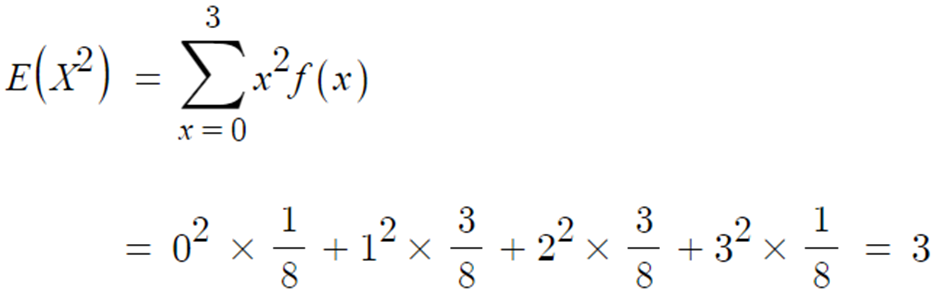
▶ 분산 Var(X)
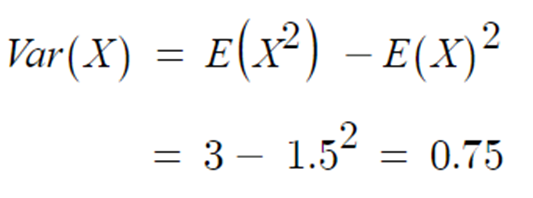
▶ 표준편차 SD(X)
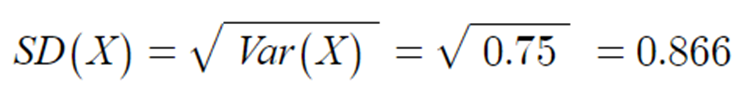
◈ 예제 : 이산균일분포(이산균등분포)
- 이산확률분포중 확률 함수가 정의된 모든 곳에서 그 값이 일정한 분포를 말한다.
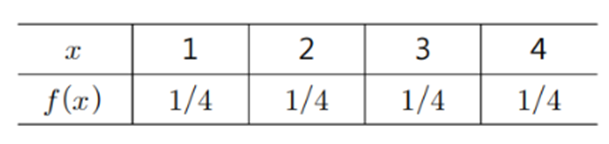
▶ 기대값 E(X)
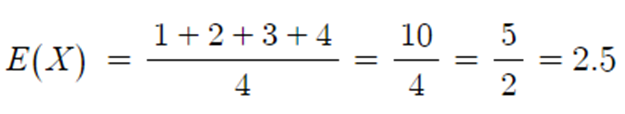
▶ 분산 Var(X)
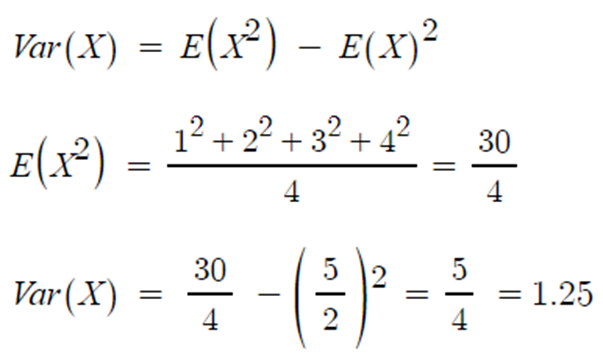
▶ 표준편차 SD(X)
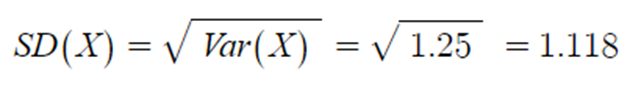
(5) 연속확률변수 X의 분산
- 앞서 Var(X)은,
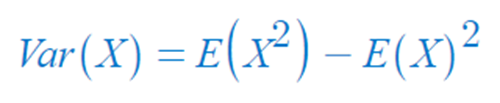
- 여기에 연속확률변수의 기대값을 대입하여 적용하면,
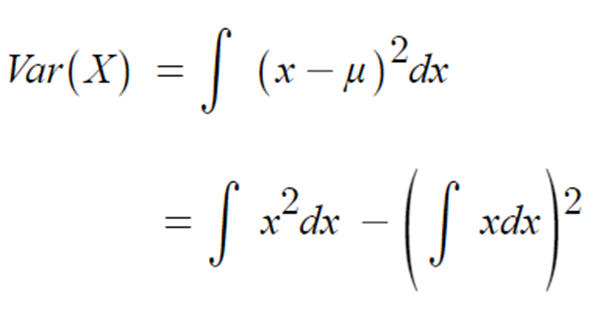
◈ 예제 : 0~12까지의 숫자가 표시된 돌림판
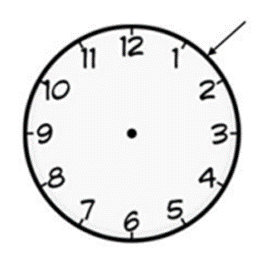
그림과 같이 바늘이 지적하는 위치를 X 라 했을 때,

▶ 기대값 E(X)
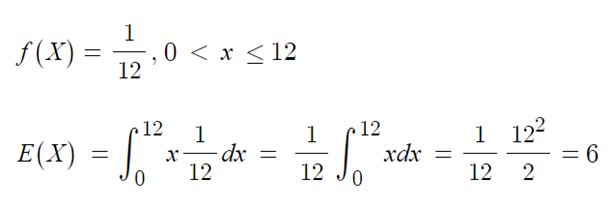
▶ 분산 Var(X)
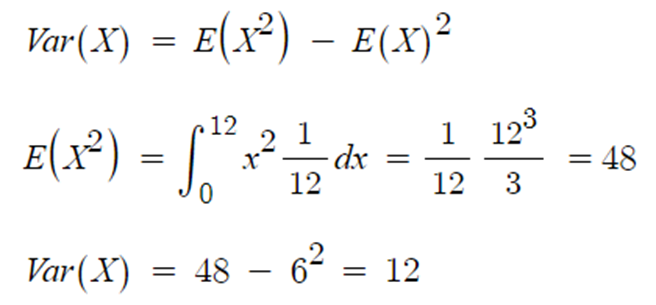
▶ 표준편차 SD(X)
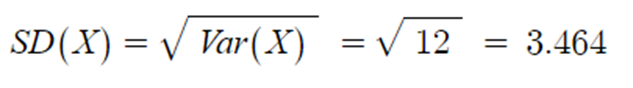
(6) 분산의 성질
- 확률변수 X의 분산을 알고 있을 때, aX+b의 분산은 얼마일까?
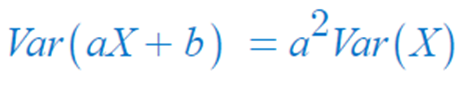
- 기대값의 성질을 이용하여 유도하면,
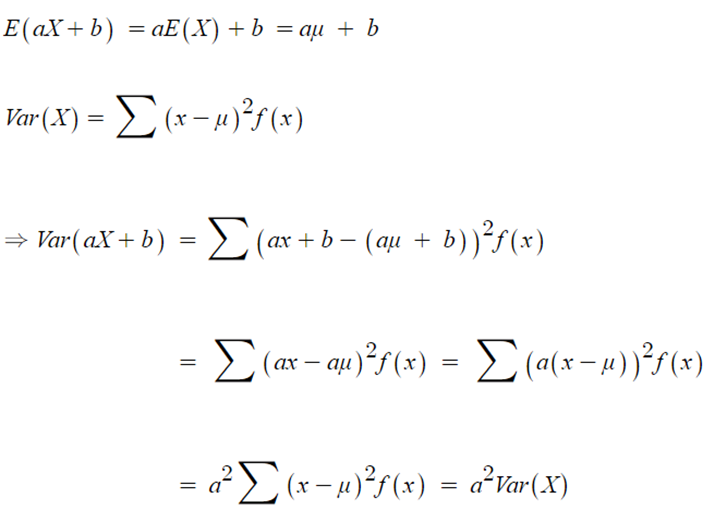
- 위치의 변화를 주는 상수 b는 분산에 영향을 주지 않는다.
- 분산은 측정단위의 제곱이기 때문에 a의 제곱을 곱한다.
▶ 표준편차 SD(aX+b)
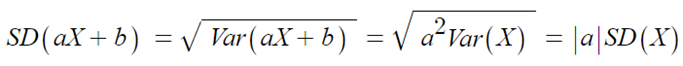
- 표준편차에서 음수는 없기 때문에 절대값으로 표기해야 한다.
◈ 예제 : 균일분포(균등분포) - Uniform distribution
- 정해진 범위에서 모든 확률이 균일한 분포를 의미한다. (통계학의 가장 기본이 되는 분포임.)
- 연속 확률 분포이며, 기호는

▶ 앞선 예제 : 0~12까지의 숫자가 표시된 돌림판의 분산을 위 분산의 성질과 균등분포를 이용하면,
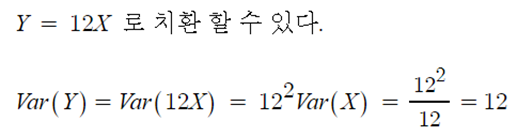
▶ W ~ (-1, 1) 로 -1 부터 1 사이가 균등분포라 한다면, W = 2X-1 로 표현할 수 있다. 따라서,
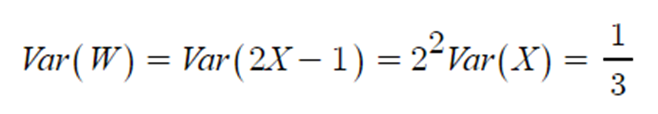
⇒ 표준 형태의 분산이 있으면 그것에서 선형으로 표시되는 것은 분산의 성질을 이용해서 쉽게 계산할 수도 있다.
'통계학 공부' 카테고리의 다른 글
| 21. 확률변수의 공분산과 상관관계 (0) | 2023.05.01 |
|---|---|
| 20. 결합분포와 주변분포 (0) | 2023.04.30 |
| 18. 확률변수의 기대값 (Expected Value) (0) | 2023.04.28 |
| 17. 확률질량함수 & 확률밀도함수 (0) | 2023.04.27 |
| 16. 확률변수와 확률분포 (0) | 2023.04.26 |




댓글