확률변수의 통계량은 확률분포를 표현하기 위한 값들이며, 이 값들은 확률함수를 통해 계산할 수 있다.
(1) 기대값 ( Expected Value)
- 확률변수에 대해 평균적으로 기대하는 값 = 모평균(population mean) ⇨ 확률분포(또는 모집단)의 무게 중심
- 하나의 확률 과정에 의해 결정되는 숫자는 하나의 값 주위로 분포한다.
- 이때 기대값(expected value)은 분포의 무게중심에 해당되는 값이다. ⇒ 기대값은 확률에서의 평균
▶ 표본평균 일반식
2023.04.17 - [통계학 공부] - 7. 수치 자료의 중심 - 평균, 중앙값, 최빈값
7. 수치 자료의 중심 - 평균, 중앙값, 최빈값
일변량 자료 요약 (1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등 (2) 범주형 - 도수분포표 (빈도수, 백분율) 다변량 자료 요약 (1) 수치형 - 공분산, 상관관계 (2) 범주형 - 분할표
pmxsg.tistory.com

◈ 예제 : {1,2,3,4,5,6}으로 이루어진 모집단으로부터 5개의 표본을 무작위로 선택 : 1,1,2,5,6
- 표본평균을 계산하면,

- 이 계산 산식을 각 관측된 값에 자료 중 그 값이 차지하는 비율을 곱하여 더한 것으로 표시하면,

- 이를 일반식으로 표현하면,

- 위의 식을 간략히 정리하면,

- 여기서 각 표본의 비율을 p로 표현하면,

▶ 기대값의 일반식
- 위에서 n이 계속 커지면,

- 기대값의 평균은 μ (뮤) 로 표기한다.
▶ 이산확률변수 X의 기대값

◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 각 확률변수의 값에 대한 확률은 아래와 같이 나타난다.

- 확률질량함수로 표현하면,

- X의 기대값은 ?

- 그림으로 표현하면,

▶ 연속확률변수 X의 기대값

◈ 예제 : 0~12까지의 숫자가 표시된 돌림판

- 그림과 같이 바늘이 지적하는 위치를 X 라 했을 때, X의 기대값은?


(2) 확률변수의 변환 (transformation)
- 확률변수의 변환은 어떤 함수를 통해서 또 다른 확률함수로 만드는 것이다.
- 이미 만들어진 확률변수 그 자체보다 변환을 해서 사용해야 하는 경우가 생길 수 있다.
- 변환된 확률변수도 여전히 확률변수 이다. 따라서, 기존의 확률변수의 성질을 그대로 가지고 있다.
- 그러므로 변환된 확률변수의 확률분포가 존재한다.
▶ 확률변수 X의 확률분포
| x | -1 | 0 | 1 | 2 |
| P(X=x) | 0.1 | 0.3 | 0.2 | 0.4 |
확률 변수 X에 제곱을 하여 변환하고, 변환한 확률변수를 W라고 한다면,
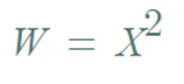
이 때 W의 확률분포를 구하려면, 기존의 확률변수 값에 연결하면 된다. 그 결과는,
| x | -1 | 0 | 1 | 2 |
| P(X=x) | 0.1 | 0.3 | 0.2 | 0.4 |
| w | 1 | 0 | 1 | 4 |
- P(W=0) = 0.3
- P(W=1) = 0.1+0.2 = 0.3 ( x의 관점에서는 -1과 1 의 값을 더한 것이다. )
- P(W=4) = 0.4
- 변환된 확률 함수 W의 기대값
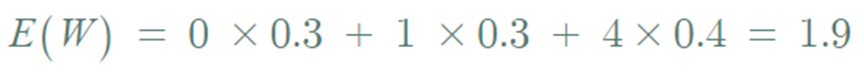
- 위의 식을 X의 관점에서 아래와 같이 표현할 수 있다.

- 이것을 일반식으로 표현하면,

- 즉, 변환전 x의 값인 -1,0,1,2를 넣으면 변형된 제곱의 값인 0,1,2의 확률에 대한 기대값으로 나온다.
▶ 일반화
- 확률변수 X의 함수 Y=g(X)의 기대값
- 이산확률변수

- 연속확률변수

(3) 기대값의 성질
▶ 임의의 상수 a의 기대값 : E(a)

▶ aX+b의 기대값 : E(aX+b)

▶ 임의의 함수 g1,g2에 대한 기대값

◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
- 각 확률변수의 값에 대한 확률은 아래와 같이 나타난다.
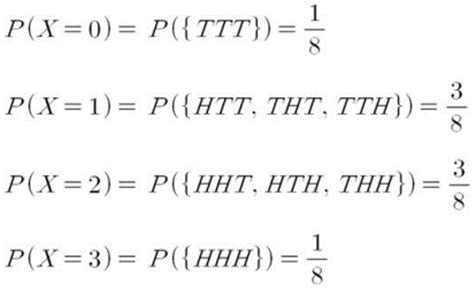
- 기대값
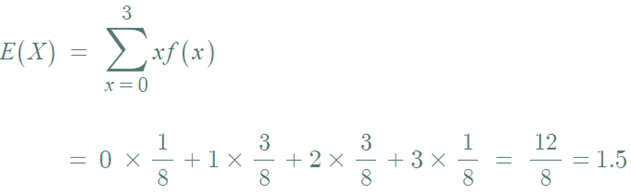
- 변형된 함수의 기대값 : x^2
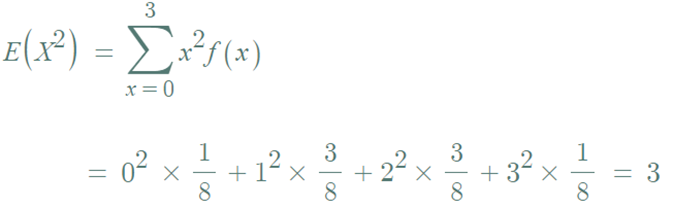
- 변형된 함수의 기대값 : ( x-1.5)^2

'통계학 공부' 카테고리의 다른 글
| 20. 결합분포와 주변분포 (0) | 2023.04.30 |
|---|---|
| 19. 확률변수의 분산과 표준편차 (0) | 2023.04.29 |
| 17. 확률질량함수 & 확률밀도함수 (0) | 2023.04.27 |
| 16. 확률변수와 확률분포 (0) | 2023.04.26 |
| 15. 조건부 확률 - 베이즈 정리 II (0) | 2023.04.25 |




댓글