(1) 확률분포의 분류
확률분포는 이산확률분포(discrete probability distribution)와 연속확률분포(continuous probability distribution)로 분류된다.
이산확률분포는 이산적인 값들을 가지는 확률변수의 분포를 의미한다. 이산확률분포는 확률변수가 취할 수 있는 값이 떨어져 있는 경우에 사용된다. 예를 들어, 동전 던지기, 주사위 던지기 등과 같이 확률변수가 취할 수 있는 값이 유한하거나 셀 수 있는 경우에 이산확률분포를 사용한다.
대표적인 이산확률분포로는 베르누이 분포, 이항 분포, 포아송 분포 등이 있다.
연속확률분포는 연속적인 값을 가지는 확률변수의 분포를 의미한다. 연속확률분포는 확률변수가 취할 수 있는 값이 연속적인 경우에 사용된다. 예를 들어, 시간, 길이, 온도 등과 같이 연속적인 값을 가지는 경우에 연속확률분포를 사용한다.
대표적인 연속확률분포로는 정규 분포, t 분포, F 분포, 카이 제곱 분포 등이 있다.
이산확률분포와 연속확률분포는 서로 다른 특징을 가지고 있으며, 각각의 특성에 따라 다른 분포를 사용해야 한다.
(2) 베르누이 분포
- 베르누이 시행 : 두 가지의 결과만을 가지는 실험을 말한다. 이러한 시행에서 각각의 결과를 성공(success)과 실패(failure)로 정의한다. (S/F) 예를 들어, 동전을 한 번 던져 앞면(H:Head)이 나오거나 뒷면(T:Tail)이 나오게 하는 것도 베르누이 시행이다.
- 베르누이 확률변수: 베르누이 시행에서 성공을 1, 실패를 0으로 정의한 이항 확률변수 중 성공과 실패 중 하나의 값을 가지는 경우를 말한다. 즉, 성공확률 p를 가지는 이항 분포에서 n=1인 경우이다. 베르누이 확률변수는 두 값 중 하나만 가질 수 있으므로 이산확률변수(discrete random variable)다.
- 베르누이 확률분포: 베르누이 확률변수의 분포를 말하며 혹은 편의상 베르누이 분포라 부른다. 이항 분포에서 n=1인 경우이며, 성공확률 p와 실패확률 q=1-p로 이루어져 있다.
▶ 베르누이 시행 (Bernoulli Trial)
- 이항분포는 베르누이 시행에서 유도된다.
- 베르누이 시행의 특징
- 각 실험에서 발생 가능한 결과는 단 2가지이다. 예) (성공,실패) , (앞면,뒷면)
- 각 실험이 독립적으로 수행한다.
- 모든 실험에서 결과의 확률은 항상 동일 예) P(S) = p , P(F) = 1-p
◈ 예시 : 불량품 검사 I
10개의 제품 중 3개가 불량품일 때,
▶ 2개를 복원 추출하는 경우.
- 실험에서 발생 가능한 결과는 2가지 이다. ⇒ 정상, 불량
- 각 실험이 독립적이다.
- 모든 실험에서 결과의 확률은 항상 동일하다.

⇒ 위 조건을 모두 충족하므로 베르누이 시행이다.
▶ 2개를 비복원 추출하는 경우.

⇒ 위 조건을 모두 충족하지 못하므로 베르누이 시행이 아니다. (모든 실험에서 결과의 확률은 항상 동일하다 는 조건을 충족하지 못한다.)
◈ 예시 : 불량품 검사 II
10,000개의 제품 중 3,000개가 불량품일 때,
▶ 2개를 복원 추출하는 경우 ⇒ 베르누이 시행

▶ 2개를 비복원 추출하는 경우.

⇒ 모집단이 크고 표본크기가 상대적으로 크지 않는 경우, 비복원 추출도 베르누이 실험을 근사모형으로 사용가능
▶ 베르누이 확률변수 (Bernoulli random variable)
- 확률변수란 원소를 숫자로 변환시켜 주는 것이다.
- 모수(성공할 확률)가 p인 베르누이 시행을 하였을 때,
- 성공이면 1로 실패하면 0으로 변환한다.
- 일종의 지시함수 (indicator function)이다.
- 즉 베르누이 확률변수는 0과 1이다.
▶ 베르누이 확률분포 (Bernoulli distribution)
- 확률분포는 확률변수가 특정값을 가질 확률이다.
- 베르누이 확률변수는 0과 1이다.
- 예 를 들면 동전던기기의 경우 𝑃(𝑋 = 0) = 𝑃(𝑋 = 1) = 0.5 확률의 법칙에 따라서 확률분포에 나온 값을 모두 합할 경 우 1이 되어야 한다. 동전던지기와 같이 2가지 가능한 결과물을 가진 확률변수의 확률분포를 베르누이 분포라고 한다
- 베르누이 확률변수의 확률질량함수는 이산 확률 변수에서 특정 값에 대한 확률을 나타내는 함수이다. 즉, 이산 확률 변수의 확률구조를 나타낸다.

- 베르누이 분포는 아래와 같이 표기한다.

▶ 베르누이 확률변수의 기대값과 분산

(3) 이항분포 (binomial distribution)
- 이항분포는 연속된 n번의 독립적 시행에서 각 시행이 확률 p를 가질 때의 이산 확률 분포이다.
- 이러한 시행은 베르누이 시행이라고 불리기도 한다. n=1일 때 이항 분포는 베르누이 분포이다.
- 대표적인 이산분포인 이항분포의 기초를 이루는 것이 베르누이 시행과 베르누이 확률변수이다.
- 즉, 이항분포는 베르누이 시행에서 유도된다.
▶ 성공할 확률이 p인 베르누이 실험을 n번 반복했을 때, 성공 횟수(X)의 분포
- X~ B(p) 라고 할 때, 성공 횟수 X는 N개의 베르누이 확률변수를 합으로 표시

▶ 이항 확률 변수
- 성공 횟수 X는 N개의 베르누이 확률변수를 합으로 표시하는데 이 때 성공 횟수 합이 이항 확률 변수이다.

⇒ X는 n과 p를 모수로 갖는 이항분포(bionominal distribution)를 따른다는 표현이다.
▶ 이항 확률 변수의 기대값, 분산
- 기대값
- 기대값의 정리 참조 : E(X+Y) = E(X)+E(Y)

- 분산
- 베르누이 시행은 독립시행
- 독립일 때 공분산은 0, Var(X+Y) = Var(X)+Var(Y)+2Cov(X,Y) : ( 공분산의 성질 참조 )

- 표준편차 SD(X)
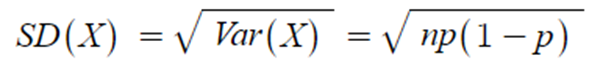
◈ 예시 : 주사위 세 번 던지기
- X = 1이 나온 횟수라 할 때, 1 이면 S(성공), 아니면 F(실패)라고 하면,

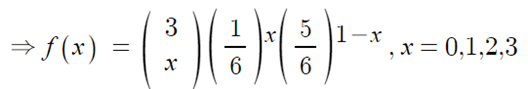
▶ 시행횟수 n, 성공확률p인 이항분포의 확률질량함수
- x는 성공횟수
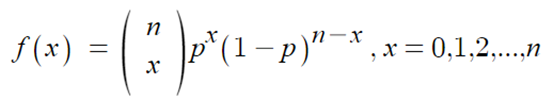
- 위 이항분포의 확률 질량 함수는 이항공식이라 표현되기도 한다.
- 조합 공식

▶ n번 시행했을 때, x번 성공할 확률은?
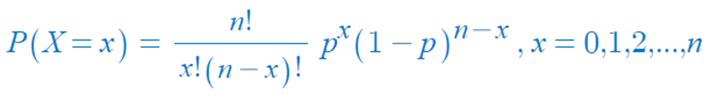
- 이항공식은 다음 조건하에서 성립한다.
- n의 값은 미리 정해져 있다.
- 매 번의 시행은 상호 독립이다.
- p는 매 시행마다 동일하다.
(4) 베르누이 (Bernoulli) vs 이항(binomial)
▶ 확률 변수
- 베르누이

- 이항
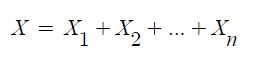
▶ 확률질량함수 (확률 분포)
- 베르누이
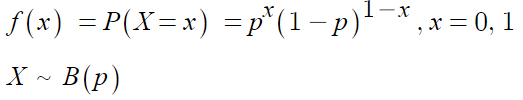
- 이항
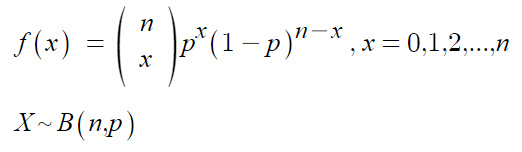
▶ 확률 변수의 기대값,분산,표준편차
- 베르누이

- 이항
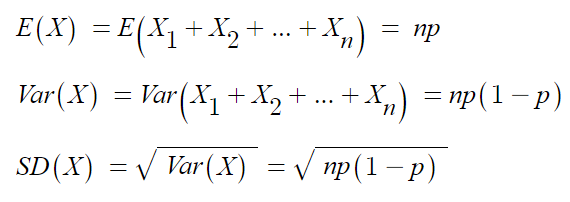
'통계학 공부' 카테고리의 다른 글
| 24. 이산확률분포 - 포아송 분포 (Poisson Distribution) (1) | 2023.05.06 |
|---|---|
| 23. 이산확률분포 - 초기하분포(Hypergeometric Distribution) (0) | 2023.05.03 |
| 21. 확률변수의 공분산과 상관관계 (0) | 2023.05.01 |
| 20. 결합분포와 주변분포 (0) | 2023.04.30 |
| 19. 확률변수의 분산과 표준편차 (0) | 2023.04.29 |




댓글