일변량 자료 요약
(1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등
(2) 범주형 - 도수분포표 (빈도수, 백분율)
다변량 자료 요약
(1) 수치형 - 공분산, 상관관계
(2) 범주형 - 분할표 (빈도수, 백분율)
(1) 산포 (dispersion, 퍼짐)
산포란 자료들이 얼마나 퍼져 있는지를 나타내는 측도이다. 중심위치와 더불어 일변량 수치형 자료 요약의 한 축이다.
데이터의 중앙을 나타내는 대표값과 더불어 데이터가 얼마나 퍼져 있는지 여부를 제시하는 대표값은 자료의 요약에 필수적인 요소이다.
대표적인 퍼짐을 나타내는 통계량은 다음과 같다.
- 범위 : 최대값 – 최소값
- IQR : 𝑄3 - 𝑄1, 여기서 𝑄1과 𝑄3는 1사분위수(하위 50%데이터의 중앙값) 과 3사분위수(상위 50%데이터의 중앙값)
- 분산 : 각 데이터가 평균에서 떨어진 거 리의 제곱의 평균
- 표준편차 : 분산의 제곱근
산포는 중심위치가 얼마나 안정적인지에 대한 중요한 정보를 제공한다.
- 자료가 조밀하게 모여있다는 것은 중심위치의 변동성이 작다는 것을 의미한다.
- 자료가 넓게 퍼져있다는 것은 중심위치(평균)의 변동성이 커진다는 것을 의미한다.
◈ 예제 데이터 : 어느 고등학교 수학 중간고사 점수
[ 98,75,46, 80,76,65,90,85,75,54,68,78,84,96,73,44,78,78,68,92,85,77,56,70,80,84,72]
(2) 범위 (Range)
자료 중 가장 큰 값과 작은 값의 차이
범위 = 최대값 - 최소값
최대값과 최소값에만 영향을 받기 때문에 자료 전체의 퍼져 있는 정도를 파악할 수 없다.
◈ 예제 데이터 : 어느 고등학교 수학 중간고사 점수
최대값 : 98 , 최소값 : 44
범위 = 98 - 44 = 54
(3) 사분위(간) 범위 (Interquartile - Range)
사분위수 (quartile) : 자료를 동일한 비율로 4등분 할 때의 세 위치
자료를 오름차순으로 정렬했을 때
- 25% 지점 : 제 1사분위수
- 50% 지점 : 제 2사분위수 = 표본중앙값
- 75% 지점 : 제 3사분위수
사분위(간)범위는 제 3사분위수와 제1사분위수의 차이
- IQR = Q3 - Q1
사분위수 계산 방법
- k=(n-1)p + 1, p = 0.25, 0.5, 0.75 계산
- k가 정수이면, x가 해당 사분위수, 아니면 비례에 의해 내삽법을 적용
◈ 예제 데이터 : 어느 고등학교 수학 중간고사 점수
- n = 27
- k = 26 x 0.25 +1 = 7.5 번째 ⇒ Q1
- k = 26 x 0.5 +1 = 14 번째 ⇒ Q2
- k = 26 x 0.75 + 1 = 21.5 째 ⇒ Q3
▶ 상자그림 (box plot)
사분위수 시각화에 사용되는 그래프이며, 자료의 주요위치 파악과 이상점 검출 등에 사용되는 그림이다.
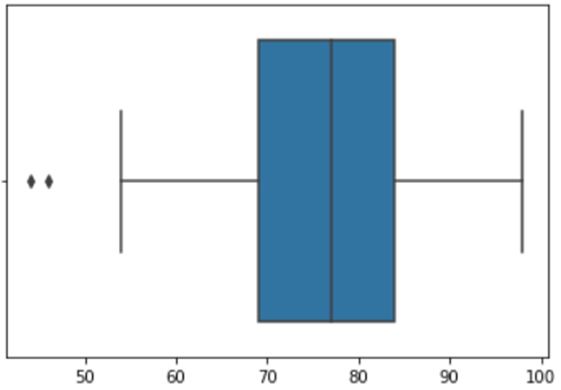
→ 왼쪽부터 최소값 , 1분위수, 2분위수(중앙값), 3분위수, 최대값을 표현한다. 예제에서 44,69,77,84,98 이다.
(4) 표본분산 (sample variance)
모든 자료들 간의 거리의 합을 이용하는 방법은?
모든 관측값들 간 거리의 합은 자료들이 넓게 퍼져 있으면 이 합들은 커질 것이고 모여 있으면 작아질 것이다.
좋은 중심위치가 되려면 자료들 간 거리가 가능한 짧아야 한다. 거리의 합을 최소로 만드는 값은 즉 편차의 합이 0인 지점이 중심위치( 평균)가 된다 .
분산은 관측값에서 중심위치(평균)를 뺀 값을 제곱하고 그것을 모두 더한 값이다. 즉, 차이값의 제곱의 평균이다.
차이값(편차)의 합은 0이 나오기 때문에 제곱을 하는 것이다.

표본분산은 n개의 편차를 사용하는 것 같지만 "편차의 합이 0 "이라는 제약조건 때문에 n-1개의 편차 정보를 사용
여기서는 n-1의 자유도 (degree of freedom)를 가진다.
자유도 (degree of freedom)는 통계적 추정을 할 때 모집단에 대한 정보를 주는 독립적인 자료의 수를 말한다.
표본 분산 산식:
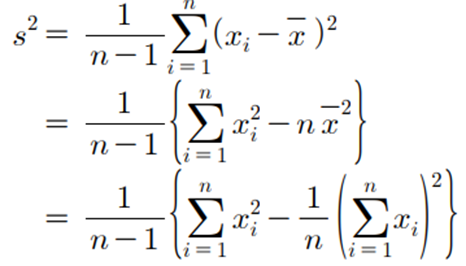
◈ 예제 데이터 : 어느 고등학교 수학 중간고사 점수 → 분산 : 183.3789
(5) 표본표준편차 (sample standard deviation)
표본분산은 편차의 제곱합을 이용하기 때문에 분산의 단위는 관측값 단위의 제곱이 된다.
눈으로 이해하는 산포와 일치하기 위해서는 자료를 측정할 때의 단위로 표시하기 위해 제곱근을 한다.
즉, 표준편차는 분산의 제곱근한 것이다. 분산의 경우 제곱의 합이어서 단위가 원 자료보다 크다. 따라서, 원 자료의 단위로 환원해주기 위해 분산에 제곱근을 한 것이다.
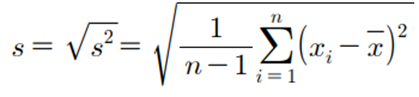
◈ 예제 데이터 : 어느 고등학교 수학 중간고사 점수 → 분산 : 13.5417
※ 자유도의 정의
- 자유도는 합쳐진 값들 중에서 실질적으로 독립인 값들의 개수이다.
- 표준편차 계산하는 경우의 자유도는 “자료의 개수 -1” 이다.
- 표준편차 계산의 대상이 되는 편차들의 합은 0이 된다.
- 편차들의 합이 0이 된다는 하나의 제약조건이 자유도를 1만큼 감소시킨 것이다.
예를들어 10개의 편차중 9개는 자유롭게 선택할 수 있지만 마지막 1개는 편차들의 합이 0이 된다는 제약조건으로 자유롭게 선택할 수 없고 정해지기 때문에 자유도가 없다는 것이다.
예를들어, 극단적으로 자료의 개수가 하나인 경우,
편차는 단 하나뿐이고 그 값은 0 이다. 0에 대해 제곱의 평균을 구할 때 자유도 고려치 않으면 0/1 = 0 이고 자유도를 고려하면 0/(1-1) = 0/0 으로 부정형(indefinite form)이 된다. 단 하나의 자료만을 가지고는 퍼진 정도를 알 수 없다. 이 때 퍼진 정도는 0이 아니라 ‘알 수 없다(부정형)’가 정답이 된다. 즉, 자유도를 고려해야 한다.
(6) 표준화(standardization)
표준화란 기준점을 동일하게 만들어 자료들을 쉽게 비교할 수 있도록 만드는 과정이다.
예를들어, 수능시험은 과목별로 난이도가 다를 수 있기 때문에 원점수로 과목간 성적을 비교할 수 없다. 이 때 표준화 점수 필요하다.
- 표준화 과정 :

- 표준화된 자료의 평균과 분산 :
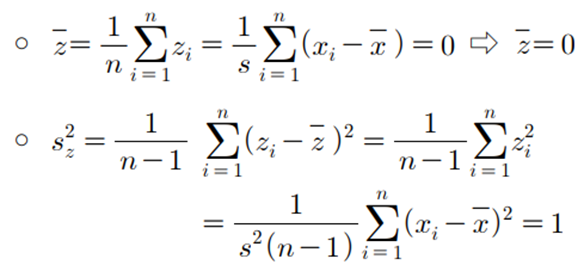
- 즉, 평균은 0 , 표준편차는 1로 조정하는 것이다.
- 표준화를 통하여 측정 단위에 영향을 받지 않게 중심위치와 척도를 조정해 절대비교 가능해진다.
(7) 변동계수(coefficient of variation)
측정단위가 서로 다른 자료를 비교하고자 할 때 사용한다. 즉, 표준편차가 평균에 영향을 받는 경우를 말한다.
예를 들어 다이어트를 할 때 체중 100kg인 사람이 10kg(10%) 감량과 50kg인 사람이 10kg(20%) 감량 했을 때, 어느 부분이 더 힘들까? 같은 10kg이라 해도 똑같이 비교 할 수 없다.
표준편차만 이용하여 산포를 비교하는 것은 적절하지 않을 수 있어 평균으로 표준편차를 보정한다.
즉, 표준편차를 표본평균으로 나눈 값을 변동계수라 한다.

100을 곱해 표본평균에 비해 표본표준편차가 얼마나 큰지를 %개념으로 표시하기도 한다.
'통계학 공부' 카테고리의 다른 글
| 10. 범주형 자료 요약 정리 - 도수분포표 & 분할표 (0) | 2023.04.20 |
|---|---|
| 9. 수치자료의 형태 - 정규분포, 왜도, 첨도 (0) | 2023.04.19 |
| 7. 수치 자료의 중심 - 평균, 중앙값, 최빈값 (0) | 2023.04.17 |
| 6. 데이터 시각화의 중요성을 알려주는 사례 (1) | 2023.04.16 |
| 5. 자료의 요약 정리 (0) | 2023.04.15 |




댓글