(1) 도대체 확률이란 무엇인가?
확률은 어떤 사건(event)이 일어날 가능성을 수학적으로 측정한 것이다.
▶ 고전적 확률(classical probability)
- 주사위 던지기와 동전 던지기와 같이 모든 결과가 나올 확률이 동일하다는 전제하에 특정 사건이 나올 확률을 계산한다.
▶ 나열 확률(enumerative probability)
- 모든 가능한 경우 를 생각하고 그 중 내가 관심이 있는 사건이 일어나는 비율을 생각한다.
- 예를 들면 검은색 공 3개와 빨간 공 2개가 들어 있는 상자에서 공을 하나 꺼낼 때 빨간 공이 나올 확률은 2/5이 다.
▶ 장기 빈도 확률(long-run frequency probability)
- 동일 한 사건이 반복적으로 일어날 때 발생하는 비율을 의미한다.
- 하지만 모든 사건이 반복적으로 일어나지는 않는다.
▶ 성향(propensity)
- 특정 사건이 일어날 진짜 가능성을 의미한다.
- 하지만 본인이 전지전능하지 않은 경우 이 “성향”을 알아내는 것은 (거의) 불가능하다.
▶ 주관적 확률(subjective probability)
- 내가 월드컵에서 한국이 4강까지 진출할 경우 10만 원을 주는 도박에 만 원을 걸었다고 하자.
- 이 경우 나의 주관적 확률은 0.1이다
▶ 확률은 다음과 같은 상황을 설명할 때 필요하다.
- 데이터가 컴퓨터(혹은 난수표)에 의해서 임의로 생성된다고 할 때
- 이미 존재하는 데이터를 임의로 선택하고자 할 때
- 임의성은 없지만 마치 데이터를 임의로 생성되었다고 가정할 때
(2) 확률변수 (Random variable)
- 동전을 던져서 앞면이 나오면 1이라 기록하고 뒷면이 나오면 0이라고 하자. 이처럼 특정 결과를 숫자와 연관시키는 규칙을 만들 수 있다. 이러한 규칙을 확률변수라고 한다.
- 구체적으로 우리가 특정 사건(동전던지기)을 생각하고 특정 사건의 가능한 모든 결과물(앞면, 뒷면)의 집합을 표본공간 (sample space)라고 한다.
- 확률변수는 이러한 표본공간에 속한 각각의 원소에 특정 숫자를 대입한 값이라고 생각하면 된다.
- 확률변수를 영어로 표현하면 Random variable. 여기서 Random은 무작위라는 의미이다.
- 확률변수의 핵심은 숫자로 변환한다는 것이다.
- 확률변수를 사용하는 이유는 이처럼 숫자로 변환하여 수학적 모형을 만들 수 있기 때문이다.
- 수학적 모형을 통해서 구체적으로 또는 계량화 된 분석을 할 수 있게 된다.
- 즉, 불확실한 현상을 수학적인 모형으로 만들 수 있는 근거를 마련하는 것이 확률변수이다.
▶ 수학적 표현
⇒ 확률변수는 표본공간에서 정의된 실함수(real-valued function: 실수의 어떤 집합의 각 원소에 하나의 실수를 대응시키는 함수)이다.
⇒ 확률변수는 정의역(출력 값을 도출하는 입력 값의 집합) 이 표본공간 Ω 이고 공역(함수의 값들이 속하는 집합)이 실수인 함수이다.
⇒ 표본공간은 확률실험에서 나왔고, 나온 원소들을 숫자로 바꿔 주는 것이 확률변수이다.
◈ 확률실험의 2가지 특징
1. 실험시작전에 모든 결과를 알 수 있다. ( 표본공간 )
2. 불확실성 (사건) - 어떠한 사건이 얼마나 일어날지는 알 수 없다.
⇒ 통계학에서는 불확실성을 가지는 사회적,자연적 현상을 일종의 확률실험으로 이해하고, 표본공간을 숫자로 표시하고 불확실한 현상을 수학적으로 모형화 하여 구체적으로 계량화된 분석하는 학문이라고 할 수 있다.
※ 통계학은 불확실성을 제거하는 것이 아니라 불확실성을 수학적으로 모델링하는 것이다. 이 모델링의 첫 단계가 숫자로 바꿔주는 함수 확률변수인 것이다.
◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 미리 알 수 있다.
- 이 때 표본공간에 있는 원소를 숫자로 바꾼다면,
- 앞면이 나오는 수를 궁금해 할 수 있고, 앞면과 뒷면의 수의 차이에 관심이 있을 수도 있다.
- 앞면의 수를 X 라는 확률변수로, 앞면과 뒷면의 수의 차이는 Y라는 확률변수로 만들 수 있다.

⇒ 이렇듯 표본공간의 원소를 숫자로 바꿔주는 것이 확률변수이다.
※ 자료의 종류에서 수치형 자료는 이산자료와 연속자료로 나누었다.
2023.04.14 - [통계학 공부] - 4. 자료의 분류와 특성
4. 자료의 분류와 특성
(1) 자료의 정의 자료 ( Data )는 문자, 숫자, 소리, 그림, 영상, 단어 등의 형태로된 의미 단위이다. 보통 연구나 조사 등의 바탕이 되는 재료를 말하며, 자료를 의미있게 정리하면 정보가 된다. 자
pmxsg.tistory.com
수치 자료(numerical data)
이산자료(discrete data)
셀 수 있는 형태의 자료 (countable data) - 예 : 충치 수, 교통사고 건수, 자녀의 수
범주형 자료의 발생빈도
연속자료(continuous data)
연속적인 속성을 가지는 자료 - 예 : 신장, 체중, 시간
표본공간에 있는 원소의 형태에 따라 확률변수의 형태가 다르게 나올 수 있다.
표본공간의 원소가 셀 수 있는 수치자료라면 즉 이산자료라면 확률변수도 셀 수 있게 나오고, 연속적인 실수형태라면 확률변수도 실수형태로 나타날 수 있다.
▶ 이산확률변수(discrete random variable) :
- 확률변수가 가질 수 있는 값들이 가산(countable) 또는 셀 수 있는 경우
- 예) 불량품의 개수, 사고 건수,...
▶ 연속확률변수(continuous random variable) :
- 가질 수 있는 값이 셀 수 없을 정도로 많은 경우
- 예) 신장, 체중, ...
(3) 확률분포 (Probability Distribution)
- 확률분포는 확률변수가 특정 값을 가질 확률을 나타낸다.
- 예를 들면 동전 던기기의 경우 𝑃(𝑋 = 0) = 𝑃(𝑋 = 1) = 0.5 확률의 법칙에 따라서 확률분포에 나온 값을 모두 합할 경우 1이 되어야 한다.
- 동전던지기와 같이 2가지 가능한 결과물을 가진 확률변수의 확률분포를 베르누이 분포라고 한다
- 확률분포를 영어로 표현하면 Probability Distribution이다. probability는 0과 1 사이라는 의미이다.
- 확률변수는 표본공간의 값을 숫자로 바꾼 함수이다.
- 확률변수가 어떤 값을 가진다는 것은 표본공간 내에 대응하는 원소들이 존재한다는 것이다.
- 확률변수는 숫자로 표시되고 해당 숫자에 대한 확률을 구할 수 있다.
⟹ 확률변수의 값에 따라 확률이 어떤 형태로 분포되어 있다는 말을 할 수 있다. 이는 그림으로 표시 가능하다.
확률분포(probability distribution)는 확률변수의 값에 대해 확률을 표시한 것이다.
◈ 예제 : 동전 3개 던지기
- 동전을 3개 던지는 확률실험을 할 때, 표본공간은 총 8개 였다.
- 확률변수 X(앞면의 수) 의 값은 0, 1, 2, 3 으로 나타난다.
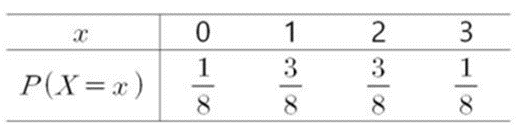
- 각 확률변수의 값에 대한 확률은 아래와 같이 나타난다.

- 이를 그림으로 나타내면 아래와 같다.

- 확률분포표(probability distribution table)는 확률변수의 확률을 표로 표시한 것이다.
▶ 확률은 모집단이 어떤 형태로 이루어져 있는지를 보여준다.
⟹ 확률분포는 모집단을 숫자로 표시했을 때의 형태이다.
즉, 확률분포는 표본의 구조가 아니라 모집단의 확률구조이다.
▶ 모집단의 확률구조를 표시하는 방법
- 이산확률변수 : 확률질량함수, 누적분포함수, …
- 연속확률변수 : 확률밀도함수, 누적분포함수, …
(4) 확률변수와 확률분포의 관계
확률변수는 특정한 값을 취할 확률을 나타내는 변수로, 확률분포는 확률변수가 갖을 수 있는 모든 값과 그 값이 나타날 확률을 나타내는 함수이다.
※ 확률변수의 모든 값 ⇒ 확률분포 ⇒ 확률변수의 확률구조 ⇒ 모집단의 형태
- 확률변수는 표본공간의 값을 숫자로 바꾼 함수이다.
- 확률변수가 어떤 값을 가진다는 것은 표본공간 내에 대응하는 원소들이 존재한다는 것이다.
- 확률변수는 숫자로 표시되고 해당 숫자에 대한 확률을 구할 수 있다.
확률변수와 확률분포의 관계는 다음 예시로 설명할 수 있다.
확률변수 X가 이산형일 경우, 확률분포는 이산확률분포로 정의된다.
예를 들어, 동전 던지기에서 앞면이 나올 확률을 p, 뒷면이 나올 확률을 1-p라고 정의할 수 있다.
이 경우, 확률변수 X는 앞면이 나오면 1, 뒷면이 나오면 0이라고 정의할 수 있다.
X가 갖을 수 있는 모든 값과 그 값이 나타날 확률, 즉 확률분포는 다음과 같이 나타낼 수 있다.
X = 0일 확률: P(X=0) = 1-p
X = 1일 확률: P(X=1) = p
이와 같이 확률변수와 확률분포는 서로 연결되어 있으며, 확률분포는 확률변수를 통해 구할 수 있다.
'통계학 공부' 카테고리의 다른 글
| 18. 확률변수의 기대값 (Expected Value) (0) | 2023.04.28 |
|---|---|
| 17. 확률질량함수 & 확률밀도함수 (0) | 2023.04.27 |
| 15. 조건부 확률 - 베이즈 정리 II (0) | 2023.04.25 |
| 14. 조건부 확률 - 베이즈 정리 (Bayes' theorem) (0) | 2023.04.24 |
| 13. 확률 - 경우의 수 (1) | 2023.04.23 |




댓글