일변량 자료 요약
(1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등
(2) 범주형 - 도수분포표 (빈도수, 백분율)
다변량 자료 요약
(1) 수치형 - 공분산, 상관관계
(2) 범주형 - 분할표 (빈도수, 백분율)
※ 다변량 변수(자료) 형태
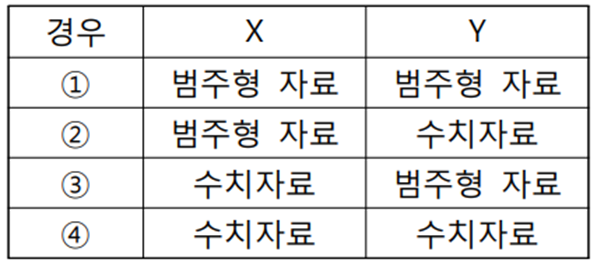
◈ 분석목적
- 비교 : X에 따라 Y에 차이가 있는가?
- 관계 : X와 Y가 관련이 있는가? X가 Y에 영향을 주는가?
- 분류 : X에 따라 Y를 분류할 수 있는가? X, Y 가 비슷한 것끼리 묶을 수 있는가?
(1) 산점도(scatter plot)
다변량 자료의 분석목적이 "관계"에 대한 분석도구로 가장 많이 사용되는 것은 산점도와 상관계수이다.
두 변수의 값을 각각 x축과 y축을 이용하여 표시나 그림을 산점도( scatter plot)이라고 한다.
▶ 자료구조와 분석목적
- 구조 : 수치자료 + 수치자료 (+..+수치자료)
- 각각의 관측개체에 대해 두 변수의 값은 순서쌍 (x,y).. 으로 표시
- 목적 : 수치 변수들 간의 관계를 유도 ⇒ 순서쌍 자료를 2차원 평면상에 점으로 표시한 그림
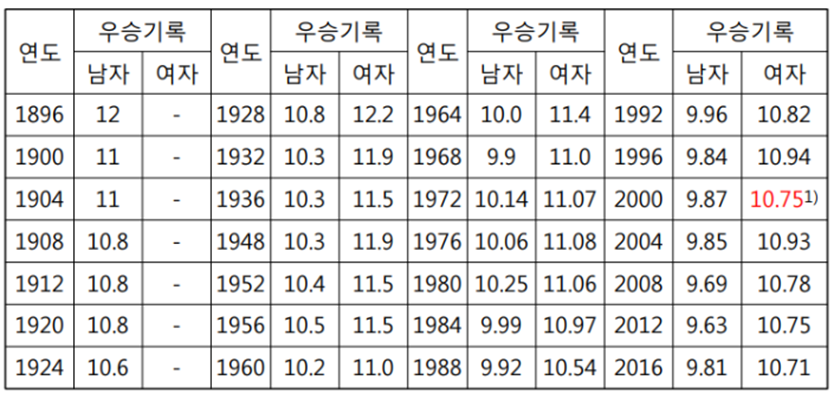
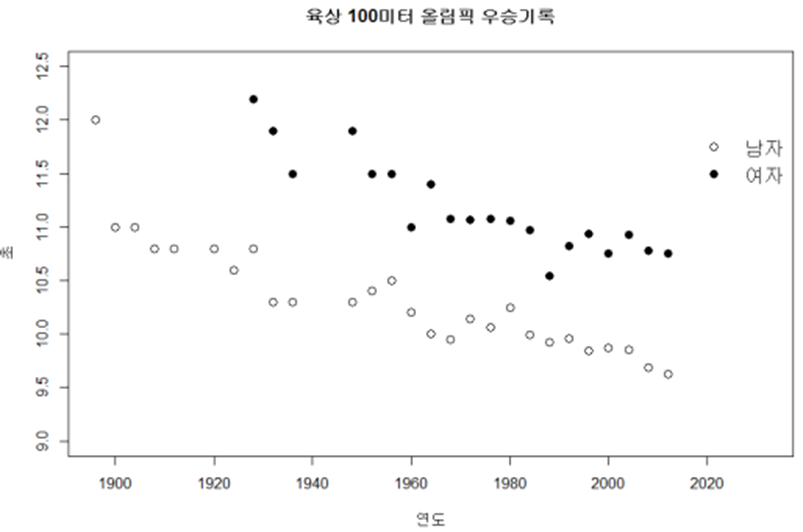
◈ 예제 : 올림픽 100미터 우승기록
(2) 상관계수(coefficient of correlation)와 공분산(covariance)
산점도와 더불어 두 변수 사이의 관계를 하나의 요약 통계량으로 나타낼 수 있을까?
라는 질문에 대한 답은 " 상관계수 " 이다.
상관계수는 두 수치변수 간에 직선관계가 어느 정도인지를 나타내는 통계값이다.
▶ 상관계수의 필요성
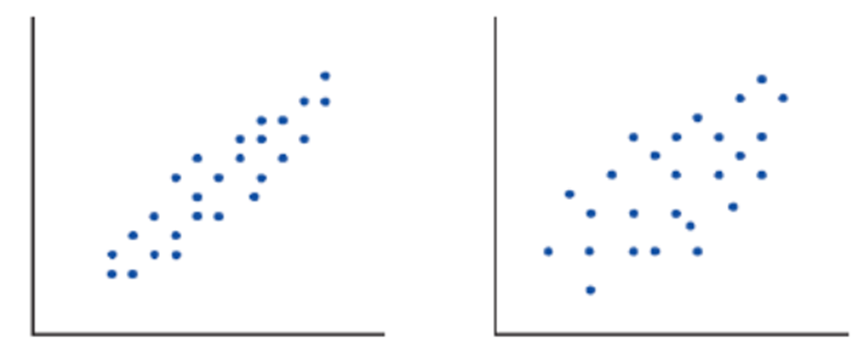
- 위의 두 산점도는 가로든 세로든 중심과 퍼진 정도가 동일하지만 왼쪽 그림이 더 강한 선형관계를 보임
- 두 변수간 선형관계의 방향과 강도가 얼마나 되는지 측정할 필요성 대두
- 상관계수는 두 변수간 선형관계의 방향과 강도 측정
▶ 양과 음의 관계를 가지는 산점도

- 위치에 따라 직선관계에는 변화가 없음 ⇒ ( x , y ) 평균을 중심으로
- 좌 그림 : ( x , y ) 평균을 중심으로 1과 3사분면에 자료가 많고 길게 분포 ⇒ 양수로 표시
- 우 그림 : ( x , y ) 평균을 중심으로 2과 4사분면에 자료가 많고 길게 분포 ⇒ 음수로 표시
- ( x , y )평균에서 멀어질수록 직선관계가 명확해짐 ⇒ ( xi -x ) ( yi -y )
(3) 표본 공분산 (sample covariance)
공분산(covariance)은 두 변수 사이의 상관 관계를 나타내는 통계량이다. 두 변수 간에 얼마나 같이 변화하는지를 나타낸다. 공분산이 양수이면 두 변수는 같은 방향으로 움직이며, 음수이면 서로 반대 방향으로 움직인다. 공분산이 0이면 두 변수는 서로 독립이다.

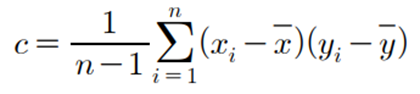
- 왼쪽 그림 : 양의 기울기인 선분에 자료가 모여 있음 ⇒ c > 0
- 오른쪽 그림 : 음의 기울기인 선분에 자료가 모여 있음 ⇒ c < 0
위의 식에서 y 를 x로 바꾸면 일변량 분산의 공식과 같다.
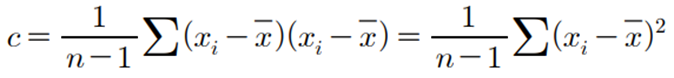
▶ 표본공분산의 간편식

◈ 예제 : 올림픽 100미터 우승기록
▶ 남자기록의 공분산

(4) 표본 상관 계수(coefficient of correlation)
상관관계(correlation)란 두 변수 간에 어떤 선형적인 관계가 있는지를 나타내는 척도이다. 두 변수 중 하나의 값이 변할 때 다른 변수도 일정하게 변화한다면, 이들은 서로 상관관계가 있다고 말할 수 있다. 상관관계는 -1부터 1까지의 값을 가지며, 1에 가까울수록 양의 상관관계, -1에 가까울수록 음의 상관관계를 나타낸다. 0에 가까울수록 두 변수 간에 상관관계가 거의 없다는 것을 의미한다.
표본 공분산의 문제점은 측정 단위에 영향을 받기 때문에 그 값 자체로 선형관계의 정도를 알 수는 없다는 점이다.
▶ 표준화된 자료의 표본공분산
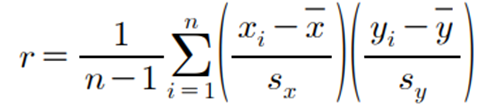
▶ 표본상관계수의 간편식 유도
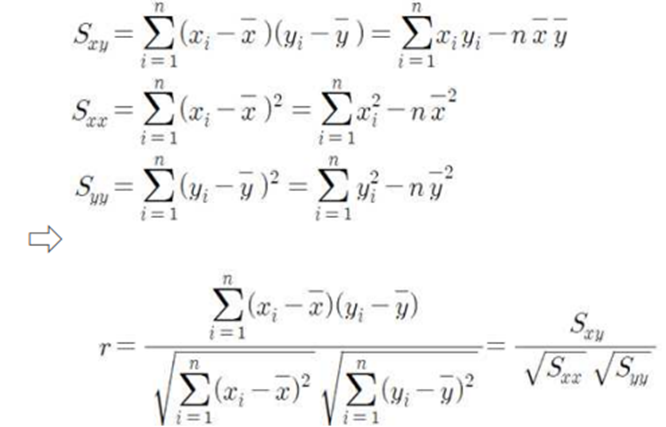
▶ 피어슨 상관계수(Pearson’s correlation coefficient)라고도 불린다. 피어슨 상관계수는 -1과 1 사이의 값을 나타내면 상관계수의 절대값이 1에 가까울수록 두 변수들이 강한 직선관계가 있음을 의미한다.
▶ 피어슨 상관계수의 한계

⇒ 위 그림은 모두 다른 모양이지만 같은 상관계수를 가진다.
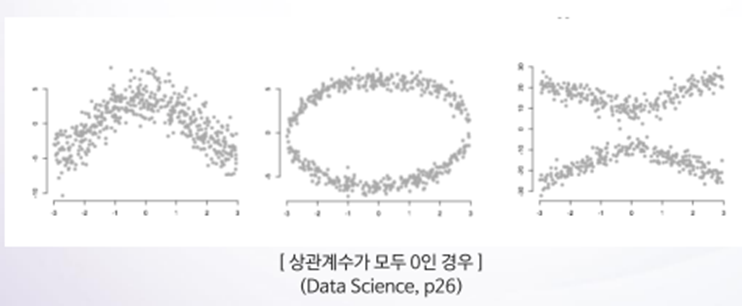
⇒ 비선형일 때는 상관계수가 0 으로 나타난다.

⇒ 이탈값(outlier)이 존재하는 경우나 두 변수간 관계가 비선형인 경우 상관계수는 유용하지 않다.
따라서, 선형일 때만 상관관계/공분산이 유용하며 상관계수가 측정할 수 있는 것은 선형관계일 때만 가능하다.
▶ 상관관계 사용 시 주의할 점
상관계수는 두 변수 간에 직선관계가 있는지를 나타낼 뿐 인과관계를 나타내는 것은 아니다.
- 예시 : 휴대전화 보급률과 기대수명에 대한 상관계수는 매우 높은 양의 상관관계를 가진다
→ 기대수명을 늘리기 위해 휴대전화 보급을 늘려야 한다 ???
- 잠복변수(lurking variable) : 두 변수에 영향을 주는 변수
→ 연도에 따라 보급률 증가, 기대수명 증가 ⇒ 허위상관 (spurious correlation)
→ 보급률과 기대수명에서 연도의 영향력을 제거하고 상관관계유도해야 한다.
◈ 예제 : 올림픽 100미터 우승기록
▶ 상관관계

⇒ 우승연도와 우승기록과는 확실한 음의 상관관계가 있다.
'통계학 공부' 카테고리의 다른 글
| 13. 확률 - 경우의 수 (1) | 2023.04.23 |
|---|---|
| 12. 확률과 통계 (0) | 2023.04.22 |
| 10. 범주형 자료 요약 정리 - 도수분포표 & 분할표 (0) | 2023.04.20 |
| 9. 수치자료의 형태 - 정규분포, 왜도, 첨도 (0) | 2023.04.19 |
| 8. 수치자료의 산포 - 분산, 표준편차, 분위수 (1) | 2023.04.18 |




댓글