확률분포의 분류
▷ 이산확률분포 : 베르누이 분포, 이항분포, 초기하분포, 포아송분포, 기하분포, 음이항분포, 다항분포 등
▷ 연속확률분포 : 정규분포, t 분포, 카이제곱분포, F 분포 등
(1) 초기하분포(Hypergeometric Distribution)
- 초기하분포(超幾何分布, hypergeometric distribution)는 이항분포와 비슷한 분포이지만, 복원추출이 아닌 비복원추출에서의 확률분포이다. 즉, 모집단에서의 성공과 실패의 비율이 변하지 않는 상황에서, 추출한 표본에서의 성공과 실패의 분포를 나타내는 분포이다.
- 초기하분포는 비복원추출에서 N개 중에 n번 추출했을 때 원하는 것 k개가 뽑힐 확률의 분포이다.
- 크기가 N인 모집단이 크기가 M과 N-M인 두 개의 부모집단 (A,B)로 나누어진 경우 ⇒ 유한모집단
- n개의 표본을 비복원으로 추출할 때, 부모집단(A)에서 추출될 표본 수의 분포 ⇒ 각 표본의 추출과정은 독립적이지 않다.
◈ 예제 : 6개가 정상품과 4개의 불량품이 있는 상자에서 임의로 3개의 제품을 비복원 추출한 경우
▶ 3개 중 1개가 불량품일 확률은 ?
- 3개 중 1개가 불량품일 사건
{ (불량,정상,정상) , (정상,불량,정상), (정상,정상,불량) }
- 확률 : P(불,정,정) + P(정,불,정) + P(정,정,불)

위 식을 분리해서 보면,
- 앞의 "3" 은 위치 중 하나를 선택해 "불량"을 대입하는 방법을 나타낸다.
- 분자는 "4"는 불량품 4개에서 1개를 비복원 추출 나열하는 방법 + "6X5" 정상품 6개에서 2개를 비복원 추출 나열하는 방법을 나타낸다
- 분모는 10개에서 3개를 비복원 추출 나열하는 방법을 나타낸다.
▶ 일반화하여 식으로 나타내면, 아래와 같다. 이 때, X는 불량품갯수를 나타낸다.

▶ 확률질량함수
- 조합공식

- 조합공식을 적용하면,

▶ 확률질량함수 일반식
- 모집단 크기 : N , M과 N-M인 두 개의 부모집단, n : 추출될 표본의 수


※ N 이 크고 N에 비해 n이 상대적으로 작은 경우
- 비복원의 효과가 적기 때문에 베르누이 실험으로 근사
- 초기하 분포는 p =M/N 인 이항분포로 근사
◈ 예시 : 10000개의 제품 중 7000개가 정상, 3000개가 불량이라면 3개를 비복원 추출에서 불량품이 한 개일 확률

※ 참조 : 이항분포의 확률질량함수

⇒ N 이 크고 N에 비해 n이 상대적으로 작은 경우 이항분포에 근사함을 알 수 있다.
(2) 초기하분포의 통계량
▶ 기대값
- 초기하분포 기대값도 각 시행에서 A집단에서 추출되면 1, 다른 집단에서 추출되면 0으로 표시한 확률변수의 합으로 표현된다.


▶ 분산

- 초기하 분포가 이항분포와 다른 점은 비복원 이므로 각각의 시행이 독립이 아니다.
- 즉, 공분산이 0 이 아니다. 따라서,

- 공분산을 알아야 한다. 공분산을 따로 살펴보면,

- 공분산의 갯수는 n개에서 2개를 조합한 것이라 할 수 있다.

- Xi 나 Xj 는 0 또는 1 이기 때문에 하나라도 0이 있으면 0이 되기 때문에 Xi가 1이고 Xj가 1일 확률만 구하면 된다.
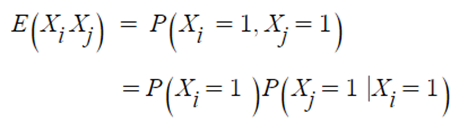

- 나온 결과값을 정리하면,
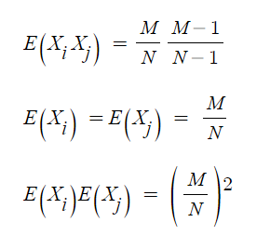
- 아래 식에 적용하면

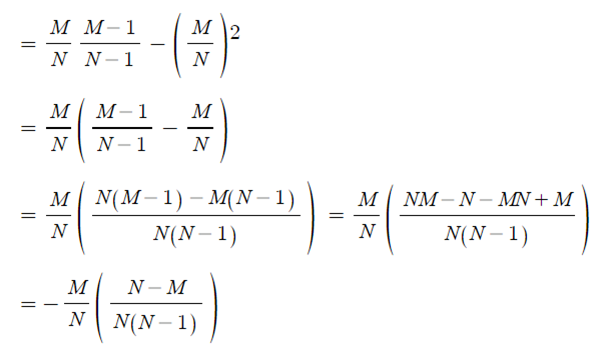
- 공분산은 아래와 같이 표현할 수 있다.

- 이제 위에서 구한 공분산을 Var(X)를 구하는 식에 대입하면,


- 위의 식을 np(1-p)를 앞으로 빼서 정리하면,
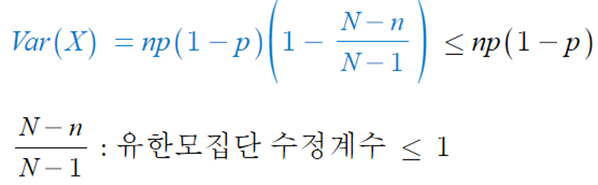
(3) 초기하분포 vs 이항분포
▶ 기대값
- 초기하

- 이항

⇒ 두 분포의 기대값은 같다.
▶ 분산
- 초기하
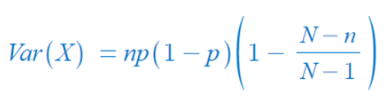
- 이항
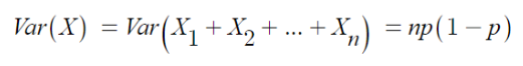
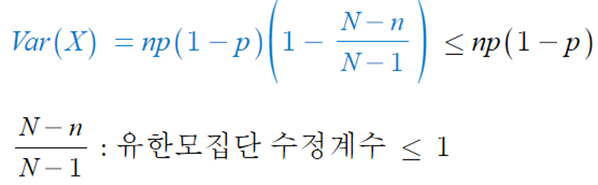
★ 초기하분포의 분산은 이항분포의 분산보다 작음을 알 수 있다.
- 분산은 퍼져있는 정도를 나타내는 데 분산이 작다는 것은 변동성이 적다고 할 수 있다.
- 그 만큼 안정적인 형태라고 볼 수 있다.
- 즉, 초기하분포가 이항분포보다 좀 더 좋은 성질을 가지고 있다는 의미이다.
- 다만 초기하분포는 보다시피 다루기가 조금 어렵다보니 이항분포로 설명하는 경우가 많을 뿐이다.
'통계학 공부' 카테고리의 다른 글
| 25. 이산확률분포 - 기하분포 & 음이항분포 (0) | 2023.05.07 |
|---|---|
| 24. 이산확률분포 - 포아송 분포 (Poisson Distribution) (1) | 2023.05.06 |
| 22. 이산확률분포 - 베르누이 분포 & 이항분포 (0) | 2023.05.02 |
| 21. 확률변수의 공분산과 상관관계 (0) | 2023.05.01 |
| 20. 결합분포와 주변분포 (0) | 2023.04.30 |




댓글