(1) 베이즈 정리 vs 고전적 확률
▶ 확률의 기원
슈발리에 드 메레 ( Chevalier de Mere)의 질문에서 시작되었다고 한다. 1650년대 프랑스 작가 슈발리에 드 메레는 다음과 같은 도박 문제를 고심하고 있었다.
- 게임 1 : 최대 4번까지 공정한 주사위를 한 개 던지는데 6이 나오면 이긴다.
- 게임 2 : 최대 24번까지 공정한 주사위를 두 개 던지는데 둘 다 6이 나오면 이긴다.
어느 게임이 더 유리한 게임일까?
이 문제에 대한 해답을 구하기 위해 드 메레가 도움을 청한 사람은 파스칼이었고 파스칼은 그의 친구 페르마와 같이 확률론의 기반을 다지게 되었다.
☆ 게임 1 : 최대 4번까지 공정한 주사위를 한 개 던지는데 6이 나 오면 이긴다.
- 여사건의 법칙에 따라 게임1의 승률은 " 1 - (4번 모두 6 이외의 숫자가 나올 확률) " 이다.
- 여기서 각각 주사위를 던질 때 나오는 눈의 개수는 서로 영향 을 주지 않으므로 곱셈의 법칙을 사용하여 (4번 모두 6 이외의 숫자가 나올 확률)은 (모두 6 이외의 숫자가 나올 확률)을 4번 곱해주면 된다.
- 따라서 게임 1의 승률은, 51.77% 이다.

☆ 게임 2 : 최대 24번까지 공정한 주사위를 두 개 던지는데 둘 다 6이 나오면 이긴다.
- 여사건의 법칙에 따라 게임2의 승률은 " 1 - (24번 모두 둘다 6이 나오지 않을 확률) " 이다.
- 여기서 둘 다 6이 나오지 않은 확률은 1 - ( 1/6 X 1/6 ) = 35/36
- 따라서 곱셈의 법칙을 사용한 게임 2의 승률은, 49.14 % 이다.

▶ 고전적 확률
고전적 확률은 주사위 던지기와 동전 던지기와 같이 모든 결과가 나올 확률이 동일하다는 전제하에 특정 사건이 나올 확률을 계산한다.
가정 : 표본공간의 각 원소(근원사건)의 발생가능성이 동일(equally likely)
- n : 표본공간의 원소개수
- k : 사건 A의 원소개수
- 사건 A의 확률 :
![]()
발생 가능성이 동일 이라는 전제가 중요 포인트이다. 빈도 확률이라고도 부른다.
▶ 베이스 정리
반면 베이즈의 정리는 고전적 확률과는 달리 조건부 확률을 기반으로 하고 있다.
베이즈의 정리는 발표 당시 18세기에는 큰 반향이 없었다고 한다. 20세기 들어서 다시 알려지기 시작하였고 1980년대 이후 몬테카를로 방법이 개발된 이후 획기적으로 응용 분야가 늘어났고 21세기에 들어 인공지능의 기계 학습이 주요한 이슈로 떠오르면서 베이즈 확률론이 적용되고 있다.
(2) 베이즈 정리 ( Bayes' theorem ) 사례
베이즈 정리는 두 확률 변수의 사전 확률과 사후 확률 사이의 관계를 나타내는 정리이다.
즉, 원인과 결과 형태의 문제에서 결과에 대한 원인 분석이 가능하게 하는 이론인 것이다.

베이즈 정리를 실제 상황에 적용시키는 일, 즉 문제를 수식화하는 것은 어려운 일인 것 같다.
그래서, 몇 가지 사례를 정리했다.
◈ 보기가 4개였던 객관식 문제를 맞추었을 때 , 알고 풀었을 확률은 얼마일까 ?
사건 A - 알고 풀었을 확률 : P(A)
사건 B - 객관식 문제를 맞추었을 확률 : P(B)
따라서, 위 문제는 P (A | B) 를 구하는 것이다.
사전확률 : 알고 풀었을 확률은 반반으로. P(A) = 1/2 로 가정한다.

알고 있었다면 맞을 확률을 1로 가정한다. 즉, P(B | A) = 1 로 한다.
모르고 찍어서 맞을 확률은 1/4 로 가정한다. (보기가 4개이므로 )
⇒ 베이즈 정리를 이용한 사후확률(posterior probability)의 계산해보면,

⇒ 보기가 4개였던 객관식 문제를 맞추었을 때 , 알고 풀었을 확률은 80% 이다.
◈ 암진단 사례
한국은 만 40세부터 2년마다 유방암 진단을 위해 유방촬영술 받기를 권장한다.
유방암 검사 시 유방촬영술의 결과는 약 90% 정확하다.
즉 암 이 있는 경우와 없는 경우를 올바르게 분류하는 것이 각각 90% 정도 정확하다는 의미이다.
검사를 받은 여성 중 1%가 실제 암이 있다고 가정하자.
(우리 나라의 유방암 환자 수는 2010년 기준 10만 명당 67.2명이다.)
유방촬영술 결과가 양성이 나올 확률은?
확률수형도 혹은 기대돗수나무 ( Probability tree ) 로 표현하면,

⇒ 1,000 명을 유방촬영술를 검사했을 때, 양성이 나온 사람은 9 + 99 = 108 명이다.
따라서, 유방촬영술 결과가 양성일 확률은 108 / 1,000 = 0.0108 즉, 1.08% 이다.
유방촬영술 결과가 양성일 때 실제 유방암에 걸려 있을 확률은 ?
⇒ 양성일 때 암에 걸려 있는 사람은 9 명이다.
따라서, 유방촬영술 결과가 양성일 때 암에 걸려 있을 확률은 9 / 108 = 0.08 즉, 8% 이다.
▶ 암에 걸렸을 때 진단 결과가 양성일 확률은 90%이지만 진단 결과가 양성일 때 암에 걸려있을 확률은 8%에 불과하다. 하지만 현실에서는 이 2가지 확률을 혼동하는 경우가 많은데 이런 유형의 혼동을 검사의 오류라고 한다.
◈ 스팸메일 필터
어떤 메일시스템의 수신메일 중 40%가 스팸메일(S)이고 나머지는 정상메일(N)이라고 한다.
스팸메일 중 25%는 “A”라는 단어를 포함하고 정상메일 중 2%가 이 단어를 포함하고 있다.
수신메일 내용 중에 "A"라는 단어가 있을 때 이 메일이 스팸메일일 확률은 ?
스팸메일을 S라 할 때, P(S) = 0.4 , 정상메일을 N이라 할 때, P(N) = 0.6 이 된다. (사전확률)
A 라는 단어가 있을 때를 사건 A라 할 때, A는 S에도 있고, N에도 있다.

수식으로 표현하면,
- 스팸메일 중 25%는 A 를 포함 ⇒ P(A | S) = 0.25
- 정상메일 중 2% 는 A를 포함 ⇒ P(A | N) = 0.02

따라서, P(A) 를 구하면,
- P(A) = 0.4 X 0.25 + 0.6 X 0.02 = 0.112
위 문제를 식으로 표현하면, P(S | A) 를 구하라라는 것이다.

즉,
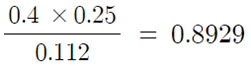
⇒ A 라는 단어가 포함되어 있을 때, 스팸메일일 확률은 89.29% 에 이른다.
◈ Secretary Problem - r passing strategy
100명의 비서 지원자가 무작위 순서로 대기하고 있다.
지원자를 순차적으로 보면서 뽑거나 말거나의 선택만 존재한다. (한번 지나가면 추후 뽑을 수는 없다).
최고 지원자를 뽑을 확률을 최대화하려면 이른바 “r passing strategy”를 구사해야 한다.
여기서 “r passing strategy” (r명 통과전략) 이란 처음 r명의 지원자는 면담만 하고 무조건 통과시킨 뒤 이후 더 나은 후보자가 나오면 곧바로 선발하는 전략이다.
1. r passing strategy 하에서 최고를 뽑을 확률은?
2. 최고를 뽑을 확률을 최대화하려면 r은 얼마여야 하나?
▶ 지원자가 4명이고 2명 통과전략을 취했을 때 최고를 뽑을 확률 , 즉, n = 4 , r = 2 일때,
- 최고를 뽑을 확률 : P(B)
- n번째 최고가 있을 확률은 P(A) 는 1/n 으로 동일 따라서 P(A) = 1/4
- 분할의 성질에 의해
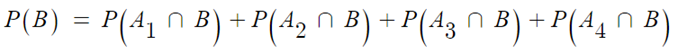
- 곱셈 법칙에 따라
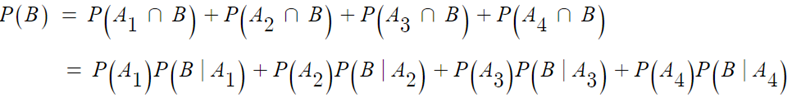
r = 2 일 때, 2개는 passing 하므로 앞선 2개의 확률은 0 이다. (기회 상실)
따라서, 뒤에 두 경우의 확률을 구하면 된다.

앞선 1,2 번째에 전체 2 등이 위치할 확률이 된다. 왜냐하면 3번째에 2 등이 위치한다면 앞선 두 사람보다 낫기 때문에 3번째를 최고로 선택하기 때문이다. 따라서 확률은 r / r+1 이 된다.
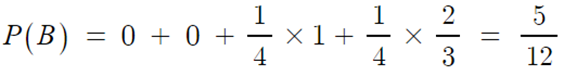
▶ 100 명의 지원자일 때

- P(B) 는 분할의 성질에 의해
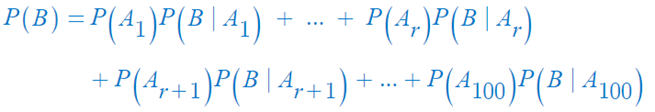
- 위 식에서, r passing 전략에 의거 1 부터 r 까지의 확률은 0 이 된다.
- P(B|Ar+1) = 1 = r/r : r+1 번째에 위치한 후보는 앞선 후보들을 모두 압도하므로 반드시 뽑히게 됨.
- P(B|Ar+2) = r/r+1 : 처음 r+1명의 후보 가운데 “국지적 최고”(전체 2등)가 처음 r의 위치에 존재하면 됨.
- 전역전 최고는 r+2번째에 위치하고 있으므로 r+1번째에서 stop하지만 않으면 반드시 전역적 최고가 뽑히게 됨.
- P(B|A100) = r/99 : 처음 99명의 후보 가운데 “국지적 최고”(전체 2등)가 처음 r의 위치에 존재하기만 하면 됨.
- 전역적 최고는 100번째에 위치하고 있으므로 r+1,...,99번째에서 stop하지만 않으면 반드시 전역적 최고가 뽑히게 됨
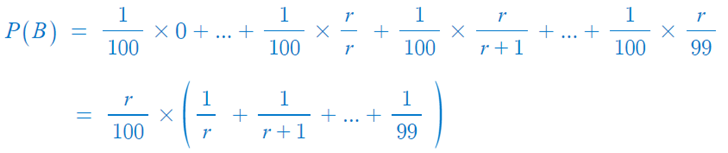
- 이제 r=1,...,99에 대해 위 식을 계산하여 가장 높은 P(B) 값을 주는 r을 구하면,
⇒ r = 37이고 이 때 최고를 뽑을 확률은 P(B) = 37% 이다.
즉, 처음 1/3 남짓의 후보는 일단 보고 나서 무조건 통과시킨 뒤 이후부터는 이미 통과시킨 사람보다 나은 후보가 있으면 반드시 채용하는 전략을 구사한다면 최고 비서 후보자를 채용할 확률은 37%씩이나 된다.
무작위로 채용하면 단지 1%의 확률과 비교하면 37배의 높은 확률을 이뤄낼 수 있는 것이다.
Secretary Problem은 응용 확률, 통계 및 결정 이론 분야에서 광범위하게 연구되는 최적 정지 이론과 관련된 시나리오를 보여준다. 최선의 선택 문제라고도 한다.
Secretary Problem는 1960년 2월 Scientific American 의 Mathematical Games 칼럼 에서 특집으로 다루었을 때 인쇄물에 처음 등장했다고 한다.
출처 : 위키백과 https://en.wikipedia.org/wiki/Secretary_problem#Deriving_the_optimal_policy
'통계학 공부' 카테고리의 다른 글
| 17. 확률질량함수 & 확률밀도함수 (0) | 2023.04.27 |
|---|---|
| 16. 확률변수와 확률분포 (0) | 2023.04.26 |
| 14. 조건부 확률 - 베이즈 정리 (Bayes' theorem) (0) | 2023.04.24 |
| 13. 확률 - 경우의 수 (1) | 2023.04.23 |
| 12. 확률과 통계 (0) | 2023.04.22 |




댓글