▶ 확률실험(random experiment) : 불확실성을 내포하고 있는 상황에서 어떤 사건이 발생할 확률을 알아내기 위한 실험
▶ 표본공간(sample space, Ω) : 확률실험에서 발생 가능한 모든 결과들의 집합
▶ 사건(event) : 표본공간 내에서의 관심 부분집합
(1) 경우의 수(the number of cases)
확률을 계산하기 위해서는 표본공간과 사건에 있는 원소의 개수를 효율적으로 계산하는 것이 중요하다.
즉, 표본공간의 크기와 사건의 크기를 알아내는 것이 필요하다.
경우의 수를 구하는 기본 법칙은 곱의 법칙 (multiplication rule) 이다.
곱셈법칙은 한 실험에서 두 개 이상의 과정이 있을 때, 각 과정마다 선택 가능한 경우의 수를 곱하여 전체 경우의 수를 구하는 방법을 말한다.
- 어떤 실험이 m 개의 연속된 단계로 이루어져 있고,
- i 번째 단계에서 발생가능한 결과의 수를 ni라 한다면,
- 전체 실험에서 발생 가능한 경우의 수는
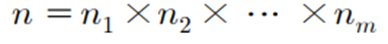
◈ 예시: 두 개의 주사위를 던져 나오는 경우의 수

⇒ 가능한 경우를 모두 나열하면 총 36 가지의 경우가 나온다. 즉, 표본공간이 36 임을 알 수 있다.
◈ 예시: 세트 메뉴 선택하기
- 세트메뉴에는 4가지 음료수, 2가지 샐러드, 5가지 메인, 4가지의 디저트 중에서 각각 하나씩을 선택한다고 했을 때,
- 선택할 수 있는 세트의 종류는,
- 4(음료수) X 2(샐러드) X 5(메인) X 4(디저트) = 160
- 총 경우의 수는 160 가지 조합을 가질 수 있다.
(2) 추출방법
◈ 1번부터 n번까지 적혀있는 공이 들어 있는 주머니에서 k개를 무작위로 선택할 때
▶ 추출방법
- 복원(with replacement) 추출
- 비복원(without replacement) 추출
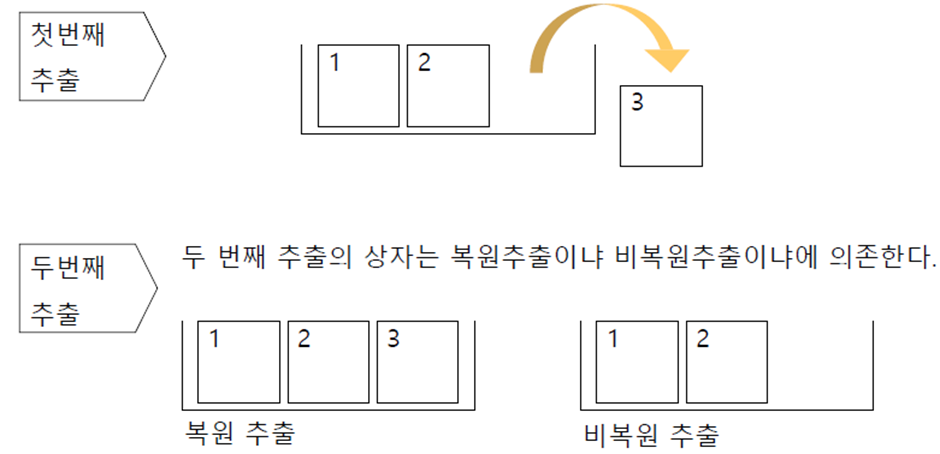
▶ 뽑힌 순서
- 순서를 고려했을 때는 (1,2)와 (2,1)을 다른 것으로 경우의 수는 2 개이다.
- 순서를 고려하지 않을 때는 (1,2)와 (2,1)을 같은 것으로 경우의 수는 1개이다.
⇒ 추출 방법과 배열 방법에 따라 경우의 수를 계산하는 방법이 다르다.
▶ 추출방법 + 뽑힌순서

A : 중복순열 , B : 순열(permutation), C : 중복조합, D : 조합(combination)
(A) 중복순열 - 복원 추출 + 순서고려
- 복원 추출이고 순서를 고려할 때의 각 회차별 경우의 수는 처음 부터 끝까지 모두 같다.
- 1회차의 경우의 수는 n이고, 2회차의 경우의 수도 n 이다. 따라서 k회차 경우의 수도 n 이다.
- 그러므로 전체 경우의 수는 n을 k번 반복하여 곱해준다. ( n x n x n x ... )
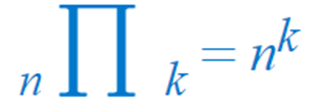
◈ 예시: (1, 2, 3, 4) 에서 3 개를 복원 추출하고, 순서도 고려할 때,
- 경우의 수는 4 x 4 x 4 = 64 개의 경우의 수가 만들어진다.
- 중복과 순서를 고려해야 하므로 ( 1,1,1),(1,1,2)...(4,4,4) 형태가 된다.
(B) 순열 (permutation) - 비복원 추출 + 순서 고려
- 비복원 추출이므로 1회차의 경우의 수는 n 이고, 2회차의 경우의 수는 n-1, k회차의 경우의 수는 n-k+1 이 된다.
- 그러므로 전체 경우의 수는 n x (n-1) x...x(n-k+1) 이 된다.
- 위의 식에 (n-k) x ( n-k-1) x ... x 1 / (n-k) x ( n-k-1) x ... x 1 을 곱해주면,
- 분자는 n x (n-1) x...x(n-k+1) x (n-k) x ( n-k-1) x ... x 1 가 된다. 즉, n!
- 분모는 (n-k) x ( n-k-1) x ... x 1가 된다. 즉, (n-k) !

◈ 예시: Birthday problem
개개인의 생월/생일을 1부터 365 가운데 하나의 숫자로 표현하자. (1월1일생은 숫자 1로, …,12월31일생은 숫자 365로) k명의 학생이 모두 다른 생일을 가지는 사건(A)의 확률을 구하라. (윤년에 태어난 학생은 없다고 가정하자.)
▶ 1 년을 365일이라고 할 때, k 명이 가질 수 있는 생일의 경우의 수 (표본공간)

▶ 사건 A : k 명의 사람이 모두 다른 생일을 가지는 사건
⇒ 1~365 숫자 중 k개를 비복원 추출로 표현할 수 있다.

▶ P (A) : 사건 A가 일어날 확률은 사건A 경우의 수를 표본공간의 경우의 수로 나눠주면 알 수 있다.


⇒ k = 23 일 때 50%를 넘기게 된다. 즉, 23명이 모여 있다면 생일이 같은 쌍이 있을 확률이 50%가 넘는다는 것을 의미하기도 한다. 50명이 모여있다면 97 %의 확률로 생일이 같은 쌍이 있다는 것을 의미한다.
(D) 조합(combination) - 순서무시 + 비복원 추출
- 비복원 추출이므로 경우의 수는 순열의 경우를 적용할 수 있다.
- 순서를 무시하기 때문에 순열의 경우의 수에서는 다른 것으로 분류하지만 조합에서는 같은 것으로 분류하게 되므로 k ! 만큼을 나눠줘야 한다.

◈ 예시 : ( 1, 2, 3, 4 ) 에서 3 개를 비복원 추출할 때,
- 순열은 4! / ( 4 - 3) ! = 24 개의 경우의 수가 만들어진다.

- 조합은 위 순열에서, (1,2,3), (1,3,2) .. (3,2,1) 등은 순서가 무시되기 때문에 하나를 대표한다.
- 따라서 조합의 경우는 4 개의 경우의 수가 만들어진다.
- 추출한 갯수가 k개라면 동일하게 간주되는 만들어 지는 수는 k ! 이다. 3개를 추출한다면 3!, 4개를 추출한다면 4!이 된다.
- 조합은 순열에서 동일하게 간주되는 갯수를 나눠주면 구할 수 있다.
( 4! /(4-3)! ) / 3 ! = 24/6 = 4
(C) 중복 조합 - 순서무시 + 복원추출
- 조합이 순열에서 k!를 나누어 구했듯이
- 직관적으로는 복원 추출이기 때문에 경우의 수는 중복 순열에서 k! 를 나누어 구하면 될 듯 하지만 이것은 오류.
◈ 예시: ( 1, 2, 3, 4 ) 에서 3 개를 복원 추출할 때, 경우의 수는 ?

⇒ 1번째의 경우의 수는 4
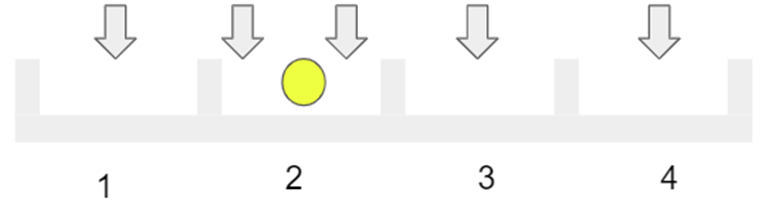
⇒ 2번째의 경우의 수는 5

⇒ 3번째의 경우의 수는 6
- 따라서, 총 경우의 수는 4 x 5 x 6 이 된다.
- 이것을 3 ! 로 나누어 주면 중복조합 경우의 수가 된다.
- 20 개의 조합이 만들어 진다.

이를 일반화 하면,
- n x (n+1) x ... x ( n+k-1 ) / k !
- 분모 분자에 1 x 2 x ...x (n-1) 에 각각 곱해주면, 분자는 (n+k-1) ! 이 되고, 분자는 k! (n-1) ! 이 된다.
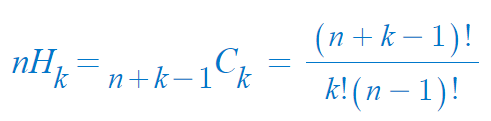
◈ 나눔 lotto 6 / 45
- 로또는 1 ~ 45 숫자 중 6개를 비복원 추출하고 순서는 무시된다.
- 따라서 조합의 경우에 해당된다.
▶ 전체 가능한 경우의 수
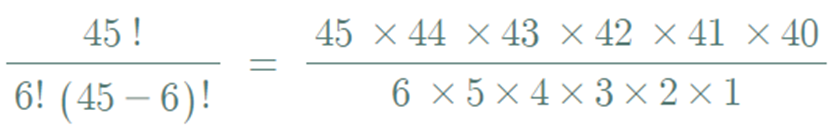
⇒ 8,145,060
▶ 1 등 당첨 경우의 수
선택한 6개의 번호가 당첨번호와 모두 일치 해야 하므로 경우의 수는 1이다.
★ 따라서 1 등 당첨 확률은 " 1 / 8,145,060 " 이다.
▶ 2,3 등 당첨 경우의 수 (보너스 번호 제외)
선택한 6개의 번호중 5개를 선택하고 나머지 하나는 다른 39개 중 하나를 선택하는 경우의 수

★ 따라서 2-3 등 당첨확률은 234/8,145,060 = " 1 / 34,807.95 "
'통계학 공부' 카테고리의 다른 글
| 15. 조건부 확률 - 베이즈 정리 II (0) | 2023.04.25 |
|---|---|
| 14. 조건부 확률 - 베이즈 정리 (Bayes' theorem) (0) | 2023.04.24 |
| 12. 확률과 통계 (0) | 2023.04.22 |
| 11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 (0) | 2023.04.21 |
| 10. 범주형 자료 요약 정리 - 도수분포표 & 분할표 (0) | 2023.04.20 |




댓글