일변량 자료 요약
(1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등
(2) 범주형 - 도수분포표 (빈도수, 백분율)
다변량 자료 요약
(1) 수치형 - 공분산, 상관관계
(2) 범주형 - 분할표 (빈도수, 백분율)
(1) 범주형 자료란
범주형 자료는 각각의 데이터가 명목상의 범주(category) 또는 서열상의 범주(ordinal) 중 하나에 속하는 자료를 말한다. 명목형 자료는 분류를 목적으로 하며, 서열형 자료는 순서를 가지고 있는 범주형 자료이다.
예를 들어, 성별, 혈액형, 종교, 결혼 여부 등은 명목형 자료이고, 학년, 선호도 등은 서열형 자료입니다.
범주형 자료를 정리할 때 변수가 하나일 때는 도수분포표를 이용하고 변수가 2개 이상일 때 분할표를 사용한다.
(2) 도수분포표 (Frequency table)
- 범주형 자료 정리 : 각 범주에 몇 개의 관측개체가 있는지를 정리한 표
- 도수 : 범주에 속한 관측개체의 수 ( =빈도)
- 상대도수 (relative frequency) : 전체 자료 중 해당 범주에 속한 자료의 비율
- 상대도수 = 해당 범주 관측개체의 수 / 전체 관측개체의 수
- 상대도수에 100을 곱해 %로 표시하기도 함.
◈ 예제 : 1 주일간 판매된 파이의 종류와 도수

▶ 수치자료의 범주화
- 자료의 값이 몇 개로 한정된 경우에는 값을 범주로 처리
- 자료를 범주화하고 도수분포표를 작성
- 순서자료 형태로 변환
- 도수, 상대도수 + (누적도수 또는 누적상대도수) 표시
▶ 범주화란 : 계급(class)의 수와 경계값(크기) 결정하는 것을 말한다.
- 계급의 수 결정 : 자료의 특성을 고려해 분석자가 결정한다. 제곱근 방법, Sturges 공식, Rice 공식 등
- 계급의 경계 : 간격(크기)과 시작점과 끝점 지정하고 동일간격이나 자료의 구조와 설명을 고려해 선택.
(3) 다변량 자료
- 다변량 자료란 변수가 2개 이상이라는 것이다.
- 통계분석 방법은 자료의 속성과 분석 목적에 따라 달라진다.
- 특히 다변량 자료 분석이 일변량과 다른 것은 분석 목적이다.
- 다변량 자료 분석의 목적은 비교, 관계, 분류 등이 있다.
- 반면 일변량 자료 분석 평균, 분산 등 기술통계량 분석이 일반적인 것으로 보인다.
- 다변량 자료 분석에서 평균, 분산 등 기술통계량을 분석하는 것은 의미가 없다. 다만 각각의 자료에 대한 평균, 분산 등 기술통계량을 비교,관계,분류 하는 방법으로 분석하는 것이다.
▶ 다변량 변수(자료) 형태

◈ 분석목적
- 비교 : X에 따라 Y에 차이가 있는가?
- 관계 : X와 Y가 관련이 있는가? X가 Y에 영향을 주는가?
- 분류 : X에 따라 Y를 분류할 수 있는가? X, Y 가 비슷한 것끼리 묶을 수 있는가?
(4) 분할표(Contingency table )
- 두 개 이상의 변수를 동시에 고려하여 각각의 범주에 관측개체의 빈도를 정리한 교차표 (cross tabulation)이다.
◈ 예제 : 세 가지 스마트폰모델에 대한 남녀별로 선호도 비교 (분석목적 - 둘 다 범주자료일 때 비교)
▶ 분할표 - 146 명에 대한 선호도 조사결과

- 남자 76명과 여자 70명을 대상으로 세 가지 모델(A, B, C) 중 가장 마음에 드는 모델을 선택
- 남자 중 모델 A는 35, B는 23, C는 18명이 선택하고 여자 중 A는 17명, B는 33, C는 20명이 선택
▶ 비율(상대도수) 표시
- 비율은 분석 목적 또는 자료가 어떻게 수집되었는지에 따라 다르게 표시
- 분모가 가능한 부분 : 성별 합계 (76,70), 스마트폰 모델별 합계 (56,56,38), 전체 합(146)
▶ 무작위로 표시한 경우 (전체 합이 분모로 했을 때 )

→ 성별과 스마트폰 선호도 간 관련성 여부는 추가로 더 분석이 필요하다.
▶ 분석목적이 선호도에서 남녀 간 차이여부일 때 (분모가 성별 합계)

→ 남자 중 각각의 모델을 선호한 비율과 여자 중 각각의 모델을 선호한 비율을 비교
→ 남성은 A 모델, 여성은 B 모델을 가장 선호한다는 것을 알 수 있다.
→ 분석 결과를 가지고 마케팅에 사용한다면 남성에게는 A 모델을, 여성에게는 B 모델을 중점으로 하는 전략을 취해야 좋은 효과가 나올 것이다.
▶ 비교 그룹별 자료 시각화
그래프를 통한 비교는 자료를 이해하는 데 도움을 준다.


◈ 예제 : 부자간의 신장(키) - 범주자료와 수치자료 일 때
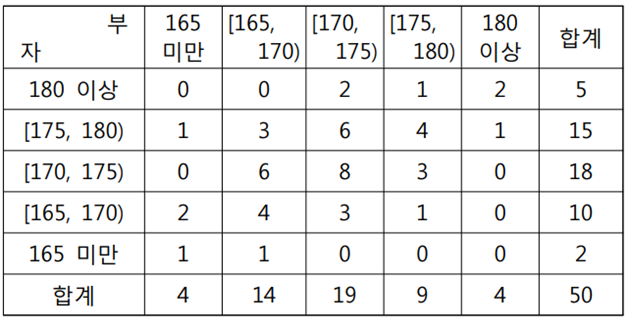
- 수치자료를 범주화하고 분할표 작성
- 분석목적이 부자간의 신장의 관계를 알아보려 했던 자료라면
- 신장 170~175 의 아버지는 총 19 명 중에 180 이상은 2명, 175~180은 6명, 170~175는 8 명, 165~170은 3명의 빈도수를 나타내고 있다는 것을 알 수 있다.
- 약 84% 가량이 아들의 키가 아버지의 키보다 크거나 같다.
(5) K-차원 분할표(K-dimensional contingency table)
- k개 범주형 변수에 대한 분할표.
- 하나의 범주가 아닌 여러 개의 범주가 존재하는 자료에 대한 분할표.
◈ 예제 : 타이타닉(RMS Titanic)호 생존자와 사망자수
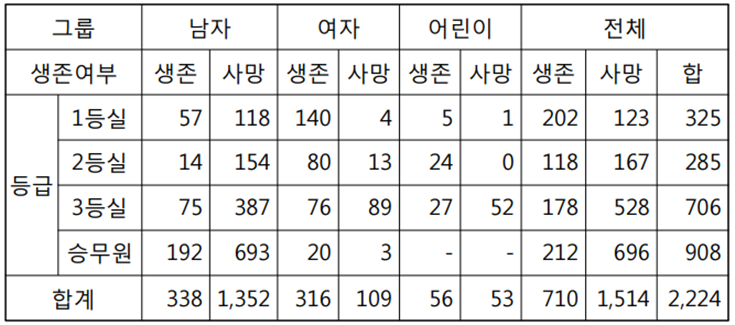
▶ 등실과 성별에 따른 생존율(%)
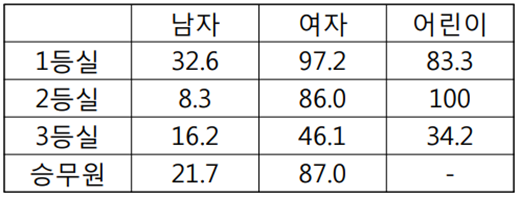
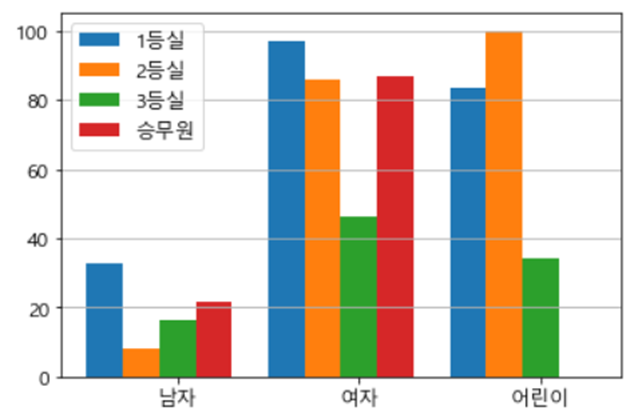
▶ 생존율
1등실 62.2%, 2등실 41.2%, 3등실 25.2%, 승무원 23.3%
남자 : 20.0%, 여자 74.4%, 어린이 : 51.4%
▶ 남녀로 구분했을 때
승무원의 생존율은 1등실을 제외한 나머지 등실의 승객보다 생존율이 높음
▶ 남성비율
1등실 54.9%, 2등실 64.4%, 3등실 73.7%, 승무원 97.5%
⇒ 분석 목적에 따라 여러 측면에서 정리할 수 있다.
⇒ 분석자료 형태와 분석 목적에 따라 분석 방법이 달라진다.
(6) 표와 그래프를 이용한 정리
자료를 표와 그래프로 정리하면 시각적으로 쉽게 이해할 수 있다. 표는 정돈된 형태로 자료를 표시하고, 그래프는 자료의 분포와 패턴을 한눈에 파악할 수 있도록 시각적으로 표현해준다. 이를 통해 자료의 특성을 빠르게 파악하고, 결론을 도출하는 데 유용하다. 또한, 다양한 그래프와 표를 이용하여 자료를 표현하면, 특정 그룹이나 패턴을 찾는 등 자료 분석에 대한 인사이트를 얻을 수 있다.
▶ 표를 이용한 정리
- 자료 구조 : 분류 (그룹 = 범주) 자료 + 수치자료
- 분석 목적 : 그룹 간 비교
- 방법 : 수치자료의 특성을 나타내는 값을 그룹별로 정리
- 기본 통계값 : 표본크기, 평균, 표준편차
▶ 그래프를 이용한 정리
- 점도표, 히스토그램(막대그래프)을 중첩, 병렬로 비교

'통계학 공부' 카테고리의 다른 글
| 12. 확률과 통계 (0) | 2023.04.22 |
|---|---|
| 11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 (0) | 2023.04.21 |
| 9. 수치자료의 형태 - 정규분포, 왜도, 첨도 (0) | 2023.04.19 |
| 8. 수치자료의 산포 - 분산, 표준편차, 분위수 (1) | 2023.04.18 |
| 7. 수치 자료의 중심 - 평균, 중앙값, 최빈값 (0) | 2023.04.17 |




댓글