일변량 자료 요약
(1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등
(2) 범주형 - 도수분포표 (빈도수, 백분율)
다변량 자료 요약
(1) 수치형 - 공분산, 상관관계
(2) 범주형 - 분할표 (빈도수, 백분율)
(1) 분포의 형태
분포란 자료가 어떤 값들을 가지고 나타나는지를 보여주는 방법이다.
자료 분포의 형태를 보면 보다 많은 정보를 얻을 수 있다. 분포 형태를 알아보는 것이 중요하다.
많은 통계분석 방법은 모집단이 중심위치를 기준으로 대칭(symmetric)이라고 가정한다.
분석방법의 적절성은 가정한 조건을 자료가 얼마나 만족하고 있는지에 따라 영향을 받는다.
자료의 분포 형태에 대한 측도를 통하여 자료가 모집단의 가정을 만족하는지에 확인한다.
(2) 분포의 형태 예시
분포의 형태는 크게 대칭 분포와 비대칭 분포로 나눌 수 있다.
대칭 분포의 대표적인 예시로는 정규 분포가 있으며, 이 분포는 평균을 중심으로 좌우 대칭의 종모양을 그린다.
비대칭 분포의 경우에는 첨도와 왜도 개념이 사용되는데, 왜도는 분포의 비대칭 정도를 나타내며, 첨도는 분포의 뾰족한 정도를 나타낸다. 대표적인 비대칭 분포로는 왼쪽으로 긴 왼쪽 비대칭 분포를 나타내는 왼쪽 치우친 분포와, 오른쪽으로 긴 오른쪽 비대칭 분포를 나타내는 오른쪽 치우친 분포가 있다.
▶ 평균과 중앙값의 관계

① 평균 > 중앙값 ② 평균 = 중앙값 ③ 평균 < 중앙값
① 평균 > 중앙값 형태의 그래프가 나타나는 경우에는 소득의 분포를 들 수 있다.
대체로 소득의 분포는 오른쪽이 늘어져 있는 형태이다. 1인당 GDP는 평균을 의미한다. 중산층의 GDP는 중앙값에 가깝다. 따라서 1인당 GDP는 중산층의 GDP보다 높다. 이유는 오른쪽으로 늘어진 히스토그램이기 때문에 즉 소수의 고소득 때문이다.
※ 우수한 학생과 열등한 학생의 이질적인 집단으로 이루어진 학급의 성적분포는 아래와 같은 그림으로 표현할 수 있다.

(3) 정규분포 (normal distribution)
- 하나의 이상적인 히스토그램이다. 하나의 수학적 모형이다.
- 개념상 모집단의 분포이다.
- 정규분포의 확률 밀도 함수 (probability density function)
- μ(뮤)를 모평균, ơ(시그마)를 모표준편차라고 부른다.
- 모집단 : 모평균과 모표준편차
- 표본 : 표본평균과 표본표준편차
▶ 정규분포곡선의 특징
- 평균을 중심으로 좌우 대칭 (symmetric)
- 종 모양(bell-shaped)
- 봉우리가 하나(Single-peaked)
(4) 표준정규분포 (standard normal distribution)
- 평균이 0이고 표준편차가 1인 정규분포 : Z ~ N(0,1)
- 즉, 정규분포를 표준화한 것이다.
표준정규분포를 사용하는 이유는,
정규분포는 평균과 표준편차의 값에 따라 분포의 형태가 달라지기 때문에, 서로 다른 평균과 표준편차를 가지는 여러 개의 정규분포를 다루기 어렵다. 이에 반해, 표준정규분포는 평균이 0이고 표준편차가 1인 공통된 분포이기 때문에, 서로 다른 평균과 표준편차를 가진 정규분포를 표준화하여 하나의 분포로 바꾸어 다룰 수 있다. 이를 통해 데이터를 쉽게 비교하고 분석할 수 있으며, 통계적인 분석에 있어서 편리성을 제공한다.
▶ 표준정규분포곡선의 68-95-99.7 법칙
- 표준단위로 -1부터 1까지 영역의 넓이 : 약 68%
- 표준단위로 -2부터 2까지 영역의 넓이 : 약 95%
- 표준단위로 -3부터 3까지 영역의 넓이 : 약 99.7%

- 약 68%의 자료가 평균으로부터 1 표준편차 범위 안에 있다.
- 약 95%의 자료가 평균으로부터 2 표준편차 범위 안에 있다.
- 약 99.7%의 자료가 평균으로부터 3 표준편차 범위 안에 있다.
- 숫자들의 약 68%가 평균으로부터 1SD이내의 영역에 존재한다. 그리고 약 95%의 숫자들이 평균으로부터 2SD이내의 영역에 존재한다. 이러한 68-95법칙은 경험적으로 많은 자료에서 성립한다.
- 개별 관측치에는 측정오차가 포함되어 있을 수 있다. 동일한 상황하에서 측정을 반복한 뒤 그 관측치들의 표준편차로 개별 관측치에 포함된 측정오차의 표준적인 크기를 추정할 수 있다.
- 정규분포곡선은 평균을 중심으로 대칭이고, 종 모양을 띠고 있으며, 봉우리가 하나이다. 정규분포곡선 아래 면적과 관련해서는 68-95-99.7 법칙이 성립한다.
◈ 예제 : 표준화 점수
학생 A와 B가 수능에서 각각 한국지리와 세계사를 선택하였을 경우 성적을 공정하게 비교할 수 있을까?
두 과목 점수의 모집단분포가 정규분포를 따른다고 가정할 수 있지만 평균과 분산은 다르다.
A는 한국지리에서 46점, B는 세계사에서 48점을 받았다고 가정하자.
한국지리를 택한 전체 수험생 점수의 평균은 40점, 표준편차는 4점이고, 세계사의 경우 평균이 42점, 표준편차가 3점이라고 하자.
두 명의 표준점수는 ?
이 경우 원 점수를 다음과 같은 절차를 거쳐서 평균이 50과 분산이 10인 표준점수로 환산하여 비교한다.
- 원 점수를 표준화(과목별 평균을 뺀 후 표준편차로 나누어 주는 작업)을 한다.
- 표준화된 점수는 평균이 0 이고 표준편차가 1인 표준정규분포를 따른다.
- 표준화된 점수를 평균이 50점이며 표준편차가 10인 표준점수로 변환한다.
- 이렇게 하기 위해 표준화된 점수에 10을 곱하고 50을 더해준다.
- A의 표준화 점수는 (46-40)/4 = 1.5 이며 표준점수의 경우 1.5X10+50 = 65점이다.
- B의 표준화 점수는 (48-42)/3 = 2 이며 표준점수의 경우 2X10+50 = 70점이다.
- 백분위수를 계산하면 A의 한국지리 점수는 93백분위수, B의 세계사 점수는 97백분위수에 해당한다.
- 수능에서 과목별 1등급을 받기 위해서는 상위 4% 즉 96백분위수 보다 점수가 높아야 한다.
- A의 점수는 2등급에 해당한다. B의 점수는 1등급에 해당한다.
세계사에서 1등급을 받기 위해서 점수는 얼마여야 하나?
- 다음과 같은 2단계 과정을 거쳐서 답변할 수 있다.
- 표준정규분포에서 96백분위수를 먼저 찾는다.
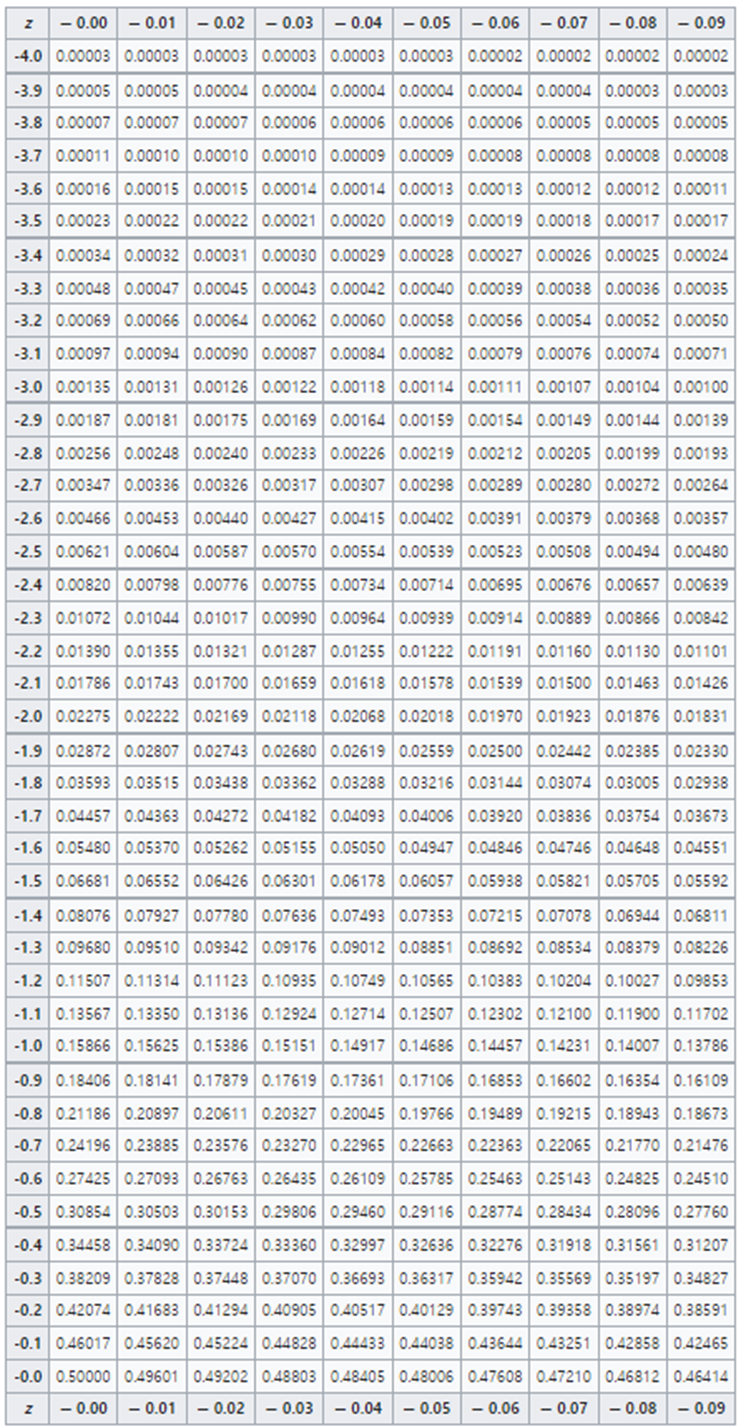
- 아래 표준정규분포표을 이용하거나 컴퓨터 프로그램을 이용할 경우 쉽게 1.75임을 알 수 있다.
- 표준점수 기준으로는 1.75 x 10 + 50 = 67.5 이며 원점수 기준으로는 1.75 x 4 +40 = 47임을 알 수 있다.
※ 표준정규분포표

(5) 왜도 (skewness)
- 자료가 대칭적으로 분포되어 있는지, 한쪽으로 기울어져 있는지에 대한 측도
- 분포가 대칭적이면 왜도는 0에 가깝다.
- 왜도는 분포의 꼬리 부분이 긴 쪽으로 치우침에 따라 양의 왜도(positive skewness) 또는 음의 왜도(negative skewness)로 나뉜다.
▶ 왜도 : 피어슨(Karl Pearson) 의 제안


- 평균보다 작으면 음수 / 크면 양수
- 평균에서 멀어질수록 큰 음수나 큰 양수가 됨
- 좌우가 비슷한 형태를 가진다면 음수와 양수가 상쇄되어 b1 은 0근처 대칭
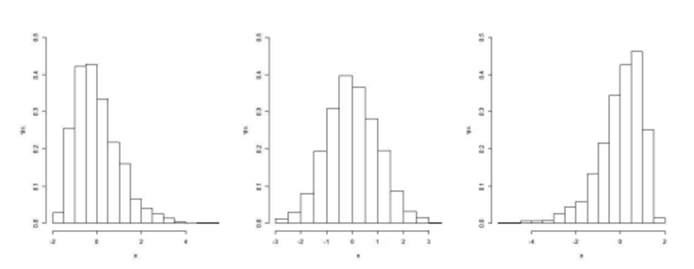
● 왼쪽 그림 :
- 오른쪽 꼬리가 길다. 즉 큰 양수값을 가진다. b1 은 대칭일 때 보다 큰 값을 가진다.
- 양의 왜도(positive skewness), skewed to the right
● 오른쪽 그림
- 왼쪽 꼬리가 길다. 즉 큰 음수값을 가진다.
- 음의 왜도(negative skewness), skewed to the left
▶ 왜도의 한계
비대칭분포에서 왜도가 가질 수 있는 문제점은 데이터가 양쪽 극단에 치우쳐져 있거나 이상점(outlier)이 포함되어 있는 경우가 있다. 이러한 경우에는 왜도가 대칭분포에 비해 큰 값으로 나타날 수 있으며, 분포의 모양을 왜곡시킬 수 있다. 따라서 왜도 값만으로는 분포의 모양을 정확히 파악하는 것이 어렵고, 첨도와 함께 고려하여 분포를 평가하는 것이 좋다. 또한 이러한 문제점을 보완하기 위해 수정된 왜도(skewness) 등의 방법이 사용될 수 있다.
수정된 왜도 :

(6) 첨도 (kurtosis)
- 양쪽꼬리가 얼마나 두터운지를 나타내는 값

▶ 첨도 : 피어슨(Karl Pearson) 의 제안


- 평균에서 멀어질수록 큰 값
- 분포의 중심보다는 꼬리부분이 얼마나 두터운지에 따라 영향을 많이 받음
- 정규분포의 경우 이론적으로는 첨도는 3

▶ 수정된 첨도

(7) 왜도 (skewness) 와 첨도 (kurtosis)의 활용
- 자료 분포의 형태를 나타내는 측도
- 심한 왜도를 가지거나 큰 첨도를 가지는 경우, 자료에 이상점이 있을 가능성이 높아진다.
- 정규성 검정 : 왜도 = 0 , 첨도 = 3
- Jacque-Bera 검정 : 정규성 검정의 한 방법

'통계학 공부' 카테고리의 다른 글
| 11. 다변량 자료의 기술 통계 - 공분산, 상관관계 & 산점도 (0) | 2023.04.21 |
|---|---|
| 10. 범주형 자료 요약 정리 - 도수분포표 & 분할표 (0) | 2023.04.20 |
| 8. 수치자료의 산포 - 분산, 표준편차, 분위수 (1) | 2023.04.18 |
| 7. 수치 자료의 중심 - 평균, 중앙값, 최빈값 (0) | 2023.04.17 |
| 6. 데이터 시각화의 중요성을 알려주는 사례 (1) | 2023.04.16 |




댓글