◈ 모집단 가정
“ 기본적으로 통계학 추론을 할 때에는 모집단에 대한 가정이 있는지 없는지 또는 그 가정이 만족하는지 안 하는지에 대해서 체크해야 한다. “
▶ 모집단이 정규분포 형태를 가질 때 T 분포를 이용하여 추론이 가능하다.
▶ 모집단이 정규분포라고 보기 어려움
* 표본크기가 큼 : 대표본
* 표본크기가 크지 않고 이상점(들)이 존재
※ 즉, 모집단의 가정에 따라 추론을 하는 방법을 달리해야 한다.
(1) 모집단이 정규성을 만족하지 않고 표본크기가 클 때
▶ 표본크기가 큰 경우이면 중심극한정리에 의해 정규분포에 근사한다.

▶ 검정 통계량은 표준정규분포에 근사한다.

▶ 대표본이라 함은 표본크기 n이 어느 정도라고 볼 수 있을까?
- n>30 이라 하지만 크다고 모두 정규분포로 되지 않는다.
▶ 구간추정
- 정규분포에서의 구간추정을 이용한다.

◈ 예제 : A 담배에 포함된 평균 니코틴 함유량 100개의 A담배를 임의 추출하여 조사한 결과 평균함유량이 0.53mg, 표준편차는 0.11mg 라고 할 때, 실제 평균 니코틴에 대한 95% 신뢰구간은 ?
- n=100, 표본이 크므로 중심극한정리에 의해 정규분포에 근사한다.

▶ 가설검정
◈ 예제 : 소비자단체에서 A담배에 포함된 니코틴 함유량이 표지에 표기된 0.5mg보다 많다고 주장한다.
- 니코틴 함유량 평균이 표기된 것보다 많은지를 5% 유의수준에서 검정하면 ?
- 귀무가설 : 니코틴 함유량이 5mg 보다 같거나 작다.
- 대립가설 : 니코틴 함유량이 5mg 보다 크다.

- 검정통계량

- 5% 유의수준에서의 분위수 : 1.645
- 비교

- 귀무가설 기각. 따라서 5% 유의수준에서 니코틴의 함유량이 표시된 니코틴 양보다 많다고 할 수 있다.
- P-value

(2) 모집단이 정규성을 만족하지 않고 표본크기가 크지 않고 이상점이 존재할 때
- 표본크기가 크지 않고 이상점이 존재할 때 이용한다.
- 비모수적 방법
- 분포에 대한 특별한 제약조건 없으며 중심위치에 대한 검정 방법이다.
▶ 부호검정 (sign test)
- 모집단의 중앙값에 대한 검정으로 관찰된 표본중에서 중앙값을 초과하는 것이 몇 개인지를 파악하는 것.
◈ 예제 : 통계학 관련학과 취업률 ( 42개 학과 무작위 선택 )

- 해당연도의 전체 대졸 취업률은 54.5% 정도가 된다고 할 때 통계학 관련학과의 취업률 평균이 전체 취업률보다 높다고 할 수 있는가?
⇒ 42개 중 28개가 54.5보다 크다. p-value = 0.0218
▶ Wilcoxon 부호순위검정 (Wilcoxon signed rank test)
- 부호 검정은 위치만 파악할 뿐 크기를 고려하지 않는다.
- 이를 보완한 검정으로 작은 거리부터 순위를 매기고 왼쪽은 - 를, 오른쪽은 + 로 주고 모두 더한 값으로 검정한다.
◈ 예제 : 통계학 관련학과 취업률 ( 42개 학과 무작위 선택 )

- 해당연도의 전체 대졸 취업률은 54.5% 정도가 된다고 할 때 통계학 관련학과의 취업률 평균이 전체 취업률보다 높다고 할 수 있는가?
⇒ 양의 부호 순위합 = 604 , p값 = 0.0287
(3) 재표집 (resampling) 방법
- 모집단 가정에 대한 특별한 제약조건 없다.
- Bootstrapping이라고도 한다.
▶ Bootstrapping의 원리

출처 : https://inferentialthinking.com/chapters/13/2/Bootstrap.html
13.2. The Bootstrap — Computational and Inferential Thinking
13.2. The Bootstrap A data scientist is using the data in a random sample to estimate an unknown parameter. She uses the sample to calculate the value of a statistic that she will use as her estimate. Once she has calculated the observed value of her stati
inferentialthinking.com
- 원래는 모집단(population)에서 표본(sample)을 여러 개 뽑는 것이지만, 여러 사정상 그럴 수 없다면 뽑아놓은 표본(sample)을 여러 번 복원추출하여 통계량을 구하는 방법이다.
- 표본(sample)에서 복원추출을 하기 때문에 중복으로 추출될 수도 있어 똑같은 표본이 생성되지 않는다. 각각의 다른 표본의 통계량을 구할 수 있다.

출처 : http://bootstrap-resampling.pdf (texample.net)
※ 표집분포 유도과정
- 모집단에서 확률표본추출 ⇒ 표본 (추정된 모집단) 에서 확률표본추출
- 통계량계산
- 위의 두 과정 반복하며 분포구성
(4) 모평균 추론을 위한 표본크기 결정
- 모수 추정을 위해서는 여러가지 표본을 수집하기 위해서 비용과 시간 등의 제약조건에 영향을 받는다.
- 표본크기는 모수 추정의 정확도 및 신뢰도에 영향을 준다.
- 따라서 모수추정을 위한 표본크기는 정확도와 신뢰도, 비용과 시간을 고려한 최적의 크기를 정해야 한다.
- 신뢰도 → 신뢰수준
- 정확도 → 오차범위 ( 오차 : 표본평균 - 모평균 )
▶ 구간 추정에 기반한 표본크기 결정방법

- 정규확률표본인 경우


- 정리하면,

◈ 예제 : 과거자료에 따르면 표준편차가 σ =5(S=5)라고 할 때,
- 95% 신뢰수준에서 오차범위가 1.5 를 넘지않는 표본크기는 ?



⇒ 최소 43개의 표본이 필요함.
▶ 가설 검정을 위한 표본크기 결정
- 가설설정
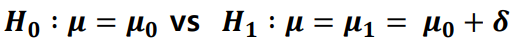

- 검정통계량

- 유의수준

- 검정력
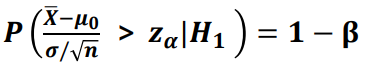
- 검정력을 달리 풀어보면,
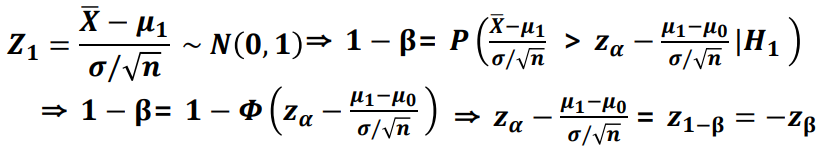
- 표본크기
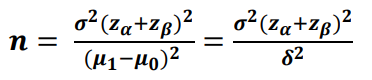
◈ 예제 : 신약개발
- 비임상(동물) 시험 이후 임상실험 (Clinical Trial)
- 1상 (Phase 1) : 약의 흡수, 대사, 배설 등의 내약성(독성)
- 2상 (Phase 2) : 용량선정
- 3상 (Phase 3) : 유효성
- 제1종 오류 : 약이 효과가 없는데 있다고 판정하는 경우 : 유의수준
- 제2종 오류 : 약이 효과가 있는데 없다고 판정하는 경우 : 검정력
- 일반적으로 5% 유의수준에서 80%이상의 검정력하에서 시험을 진행
▶ 새로운 진통제에 대한 예비연구에서 복용 전과후의 VAS차이는 평균 5이고 표준편차 10 이었다고 하자.
5% 유의수준과 80% 검정력으로 유효성 평가를 하려면 몇 명의 피험자를 대상으로 임상시험을 진행해야 하는가?

⇒ 최소 32명이 필요하다. 다만, 임상실험 탈락율은 통상 20% 이다. 따라서 탈락율을 감안하면,
32 / (1-0.2) = 32/0.8 = 40
⇒ 피실험자는 최소 40명이 필요하다.
'통계학 공부' 카테고리의 다른 글
| 37. 모비율에 대한 통계적 추론 & 정규근사 (0) | 2023.05.19 |
|---|---|
| 36. 모분산에 대한 통계적 추론 & 카이제곱분포 (0) | 2023.05.18 |
| 34. 모평균에 대한 통계적 추론 & T분포 (1) | 2023.05.16 |
| 33. 가설검정 (Hypothesis testing) (0) | 2023.05.15 |
| 32. 추정 (Estimation) (0) | 2023.05.14 |




댓글