(1) 모분산에 대한 통계적 추론
- 모분산에 대한 통계적 추론은 표본을 사용하여 모집단의 분산에 대한 추론을 수행하는 과정을 말한다.
- 이를 통해 모집단의 분산에 대한 정보를 얻을 수 있고, 추론 결과를 통해 모집단의 분산에 대한 결론을 도출할 수 있다.
- 통계적 추론에서 모분산에 대한 추론은 주로 가설 검정과 구간 추정의 형태로 이루어진다.
- 구간 추정은 모분산에 대한 신뢰구간을 구하여 모수의 추정 범위를 제공합니다. 즉, 표본을 사용하여 계산한 신뢰구간을 통해 모집단의 분산이 존재할 가능성을 추정하는 것입니다. 이를 통해 모분산의 신뢰구간을 구성하고, 모집단의 분산에 대한 추론을 수행할 수 있다.
- 가설 검정은 모집단의 분산에 대한 가설을 설정하고, 표본을 통해 얻은 통계량을 사용하여 가설을 검정하는 과정이다. 대표적인 예로는 분산의 크기가 특정 값과 같은지 여부를 검정하는 분산 검정이 있다.
- 모분산에 대한 통계적 추론은 데이터의 변동성에 대한 추정과 관련된 중요한 분야입니다. 이를 통해 표본을 통해 얻은 정보를 활용하여 모집단의 분산에 대한 결론을 도출하고, 신뢰성 있는 추론을 수행할 수 있다.
- 모평균 추론에서와 같이 모분산추론을 위해서 중심축량에 대해 알아야 한다. 중심축량은 점추정을 통해 구하는 데 직관적인 추정량으로 표본분산 및 표본표준편차를 사용한다.
- 따라서 분산과 표준편차의 구간추정과 가설검정을 시행함으로 추론할 수 있다.
- 기본적으로 우리가 분산에 대한 추론을 할 때 모집단에 대한 가정은 정규분포를 가정한다.
- 따라서 정규분포를 만족하는지 안하는지 확인할 필요가 있다. 정규분포가 아닌 경우에 약간 문제가 발생할 수도 있다.
▶ 표본분산의 통계적 성질

- 점추정량 : 모분산, 모표준편차는 표본분산,표본표준편차로 사용가능

▶ 점추정량의 통계적 성질
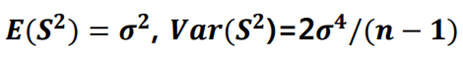
- 수정제곱합을 분산으로 나누면, 카이제곱분포를 따른다고 알려져 있다.


▶ 중심축량

(2) 카이제곱분포(chi-square distribution)
- 카이제곱분포는 자유도(parameter)를 가지는 특정한 확률분포다. 주로 분산 분석, 카이제곱 검정, 신뢰구간 추정 등 통계적 분석에서 사용된다.
- 카이제곱분포는 정규분포로부터 독립적으로 추출한 n개의 표준정규분포를 제곱하여 합한 값을 따른다. 따라서 카이제곱분포의 모양은 양수 값만을 가지며, 왼쪽으로 긴 꼬리를 가진다.
- 카이제곱분포의 모양은 자유도에 의해 결정된다. 자유도는 독립적인 표준정규분포의 개수로서, 카이제곱분포의 형태와 분산을 조절하는 역할을 한다. 자유도가 작을수록 분포의 모양은 더 울퉁불퉁하고 왼쪽으로 치우친다. 그러나 자유도가 증가할수록 분포는 더 정규분포에 가까워진다.
- 카이제곱분포는 주로 분산 분석에서 잔차의 분포를 가정할 때 사용되며, 카이제곱검정에서도 사용된다. 또한, 모집단의 분산에 대한 신뢰구간을 추정하기 위해서 카이제곱분포를 활용할 수 있다.
▶ 자유도에 따른 카이제곱분포 형태
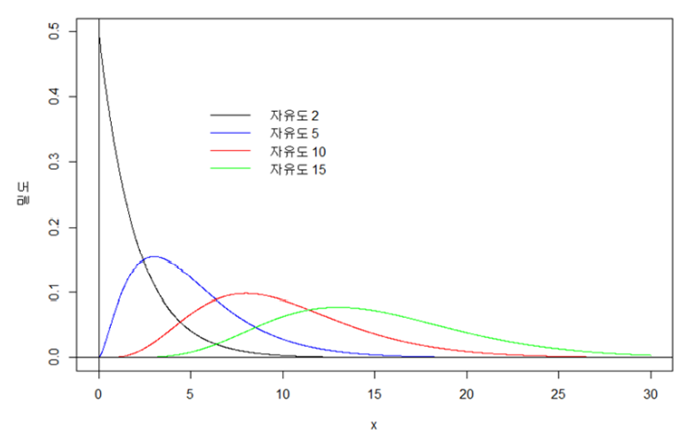
▶ 카이제곱분포의 특징
- 대칭이 될 수 없다. 구간 자체가 0보다 커야하기 때문에.
- 자유도에 따라 다양한 형태의 그림이 나온다.
- 자유가도 크면 클수록 옆으로 더 퍼지는 형태가 나온다.
- k개의 서로 독립적인 표준정규확률변수를 각각 제곱한 다음 합해서 얻어지는 분포이다.
- k를 자유도라고 하며 카이제곱분포의 매개변수가 된다. 카이제곱분포는 신뢰구간이나 가설검정에서 사용한다.
- 정의 : 표분정규분포를 따르는 확률변수의 제곱이 자유도가 1인 카이제곱분포를 따른다.
- 서로 독립인 카이제곱분포의 합은 역시 카이제곱분포를 따르며 이 경우 자유도는 합치기 전 각각 확률변수의 자유도의 합과 같다.
▶ 카이제곱분포에서의 분위수


- 구간추정을 할 때 가능한 짧은 구간을 선호한다.
- 위 두 구간중 위의 것(빨간라인)이 구간이 짧지만 계산하기가 상당히 어렵다.
- 따라서 0.025가 되는 구간(파란라인)을 찾고 여기에 해당되는 임계값을 일반적으로 사용한다.
(3) 모분산의 구간추정
▶ 모분산의 100(1-α ) % 신뢰구간
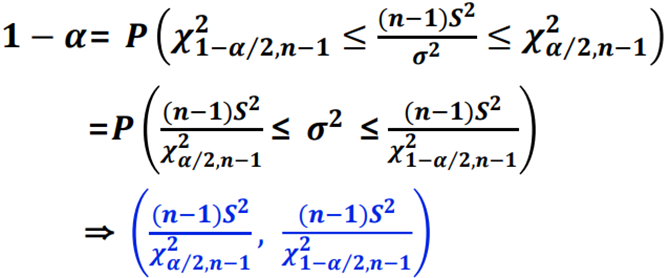
▶ 따라서 모표준편차의 100(1-α ) % 신뢰구간
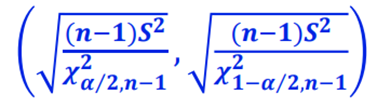
▶ 자유도에 따른 카이제곱 분포표

◈ 예제 : 제품강도
- 생산된 제품의 강도가 어느 수준에서 안정적으로 생산되는지 알아보기 위해 임의로 8개를 선택하여 제품강도를 측정함.
- 안정성은 분산으로 평가한다.
- 제품 강도 결과 : 24.3 , 28.6, 30.2, 26.5, 25.7, 27.8, 26.9, 29.0
▶ 모분산과 모표준편차의 95% 신뢰구간은 ?
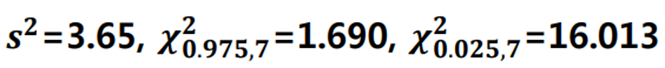
- 모분산 95% 신뢰구간
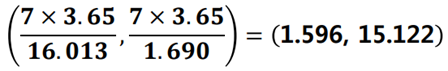
- 모표준편차 95% 신뢰구간

(4) 가설검정
▶ 가설검정의 절차
① 가설설정
- 귀무가설 : 현상태에 대한 잠정적 가정
- 대립가설 : 우리가 알고 싶은 것
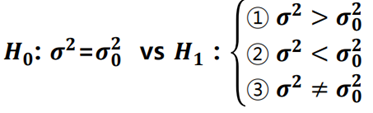
② 검정통계량
- 귀무가설하에서 표본의 비정상성을 결정하기 위해 사용하는 통계량

③ 검정통계량의 확률분포와 유의수준을 비교 검토한다.

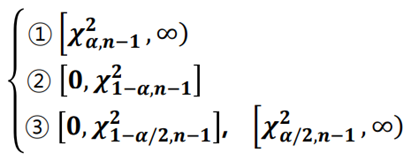
④ 결론
- 기각역 : 비정상영역 ⇒ 귀무가설 기각 ( 대립가설 채택 )
- 채택역 : 정상영역 ⇒ 귀무가설 유지 ( 대립가설 기각 )
※ 카이제곱검정에서 검정통계량은 각 칸에서 (관측값-기대값)^2/관측값을 계산하고 이 값을 모두 합한 것으로 정의된다.
※ P-value를 구하기 위해서 귀무가설하에서 검정통계량의 분포를 알아야 하는데 이 분포는 카이제곱분포를 따른다.
◈ 예제 : 제품강도
- 표준편차가 2미만일 때 안정적인 품질관리가 유지된다고 할 때 품질관리가 유지되는지 검정
- 가설 설정 : 분산은 표준편차의 제곱으로 표현한다.

- 검정통계량

- 기각역

- 비교

- 결론 : 검정통계량 6.389 > 2.167 이므로 기각역 밖에 있으므로 귀무가설을 기각할 수 없다.
- 5% 유의수준에서 안정적인 품질관리가 유지되고 있다고 할 수 없다.
'통계학 공부' 카테고리의 다른 글
| 38. 두 모집단 비교 - 모평균 비교 I (0) | 2023.05.24 |
|---|---|
| 37. 모비율에 대한 통계적 추론 & 정규근사 (0) | 2023.05.19 |
| 35. 모평균에 대한 통계적 추론 II (0) | 2023.05.17 |
| 34. 모평균에 대한 통계적 추론 & T분포 (1) | 2023.05.16 |
| 33. 가설검정 (Hypothesis testing) (0) | 2023.05.15 |




댓글