모평균의 통계적 추론은 표본을 통해 모집단의 평균에 대한 정보를 얻고자 하는 과정이다. 일반적으로, 통계적 추론은 모집단의 평균에 대한 추정과 가설 검정 두 가지로 나눌 수 있다.
▶ 모평균에 대한 추정:
- 표본을 통해 모집단의 평균을 추정하는 것을 말한다.
- 대표적으로 표본평균을 사용하여 모평균을 추정하는 방법이 있다.
- 추정량인 표본평균을 이용하여 모평균의 구간추정을 수행할 수 있다. 이를 통해 모평균이 어느 범위에 있을 것으로 예측할 수 있다.
▶ 모평균에 대한 가설 검정
- 모집단의 평균에 대한 가설을 세우고, 표본을 통해 가설을 검정하는 것이다.
- 가설 검정에서는 주로 귀무가설(H0)과 대립가설(H1)을 설정하고, 표본을 분석하여 귀무가설을 기각할지 채택할지를 결정합니다.
- 일반적으로 가설 검정에서는 유의수준을 설정하고, p-value를 계산하여 유의수준과 비교하여 결정합니다.
모평균의 통계적 추론은 표본 데이터를 통해 모집단의 평균에 대한 정보를 추론하는 중요한 방법이다. 이를 통해 모집단에 대한 정보를 얻고, 의사결정이나 추론에 활용할 수 있다.
◈ 모집단 가정
“ 기본적으로 통계학 추론을 할 때에는 모집단에 대한 가정이 있는지 없는지 또는 그 가정이 만족하는지 안 하는지에 대해서 체크해야 한다. “
▶ 모집단이 정규분포 형태를 가짐
▶모집단이 정규분포라고 보기 어려움
- 표본크기가 큼 : 대표본
- 표본크기가 크지 않고 이상점(들)이 존재
※ 즉, 모집단의 가정에 따라 추론을 하는 방법을 달리해야 한다.
(1) 정규 모집단 가정 했을 때
▶ 정규성 가정의 적절성 확인필요
- 정규성 확인 방법 : Shapiro-Wilk Test, Jacque-Bera test, ...
- R 등 통계프로그램을 통해 확인해 볼 수 있다.
- 정규분포의 가정을 데이터가 적절히 만족하는지를 확인 필요하다.
▶ 확률표본
- 정규 모집단에서 추출한 확률표본은 정규분포를 나타낸다.

- 대체표현-표준화를 하면 표준정규분포를 나타낸다.

▶ 점추정
- 모수인 모평균에 대한 정보는 표본평균이 가장 많이 가지고 있으므로 직관적으로 표본평균을 사용한다.
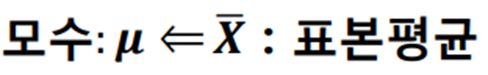
▶ 표본평균의 성질
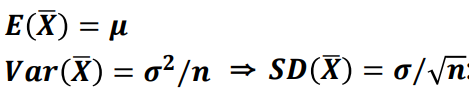
- 표본평균의 표준편차는 표준오차(Standard Error, S.E)이다. (이 확률표본은 표집분포이기 때문이다.)
- 이때 확률분포는,

- 모집단의 분산과 표준편차는 모르는 경우가 많다 따라서, 모표준편차 대신에 표본표준편차(S)를 사용한다.
- 중심축량의 정확한 분포는 알지 못한다.
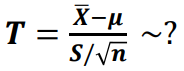
(2) T 분포
- T-분포는 student T-분포의 줄임말로 맥주회사 기네스사에 일하던 월리엄 고셋이 1908년에 제안하였는데 회사의 방침에 따라 본명을 사용할 수 없었던 고셋이 "student"라는 필명을 사용하여 제안하였다.
- T-분포는 모집단의 표준편차를 알지 못할 때, 모집단이 정규분포를 따르는 경우에 사용한다. 표본의 크기가 작을수록 모집단의 표준편차를 정확하게 추정하기 어렵기 때문에, 이러한 상황에서 T-분포를 사용하여 통계적 추론을 수행한다.
- T-분포는 자유도(degree of freedom)라는 개념에 기반하여 정의된다. 자유도는 표본의 크기에 따라 결정되며, 표본 크기가 작을수록 자유도가 작아진다. T-분포는 표본 크기가 커질수록 표준정규분포에 수렴하게 되며, 표본 크기가 작을 때는 보다 두꺼운 꼬리(tail)를 가진 분포를 보이게 된다.
- T-분포는 평균이 0이고 표준편차가 1인 표준정규분포를 따르는 확률변수를 자유도로 나눈 분포로 정의된다. 이러한 정의에 따라 T-분포의 확률밀도함수는 자유도에 따라 달라지며, T-분포의 특성을 나타내는 t-값을 계산하여 가설 검정 등의 통계적 추론을 수행한다.
▶ 표본표준편차를 이용한 중심축량

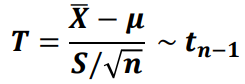
▶ T분포의 확률밀도함수
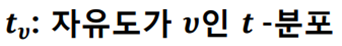
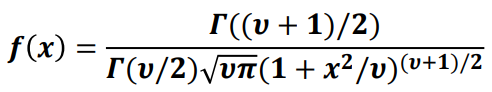

- T-분포는 정규분포와 비슷한 모양으로 0을 중심으로 대칭이며 꼬리부분이 보다 두터운 모양을 가진다.
- 전체 면적이 1이 되어야 되기 때문에 가운데 부분이 낮아지면 꼬리부분이 두꺼워진다.
- T-분포의 모수는 자유도 하나이며 자유도가 커질수록 정규분포와 흡사한 모양을 가진다.
▶ T-분포 확률 및 분위수 계산
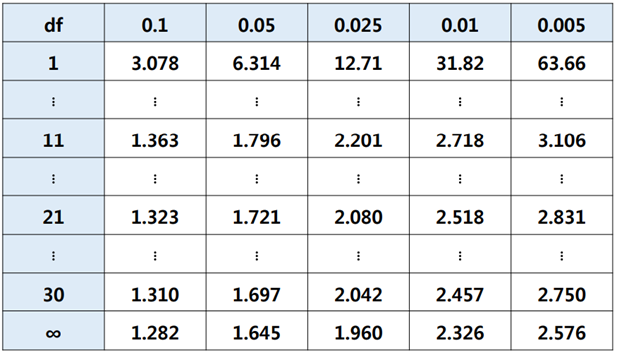
- T-분포의 경우에는 자유도에 따라 다양한 확률을 가지고 있기 때문에 하나의 표로 모든 확률을 표시할 수 없다.
- R 등 통계프로그램을 이용해 확률을 확인해 볼 수 있다.
▶ T-분포 활용
- T-분포는 모집단의 분산(혹은 표준편차)이 알려져 있지 않은 경우에 정규분포대신 이용하는 확률분포이다.
- T-분포도 표본평균,표본분산으로 정의되는 확률변수이기 때문에 표본의 수가 많아질수록 ‘중심극한정리’에 의해 결국 정규분포에 수렴한다.
- T-분포는 정규분포의 평균을 측정할 때 주로 사용되는 분포이다.
(3) 추정
▶ 중심축량 : 표본평균과 표본표준편차를 이용
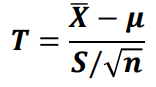
▶ 모평균의 구간추정
- 유도과정
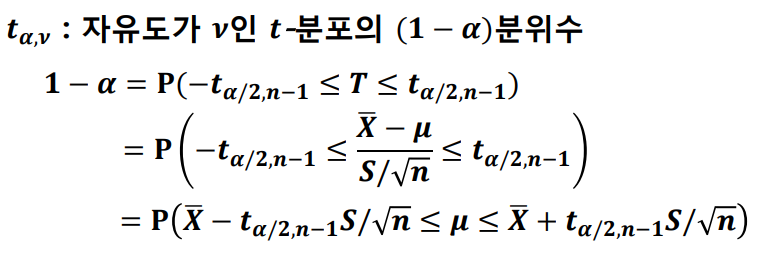
- 100 (1 - α) % 신뢰구간

◈ 예제 : 통계학 관련학과 취업률 ( 42개 학과 무작위 선택 )

- 통계학 관련학과의 평균취업률에 대한 95% 신뢰구간은?

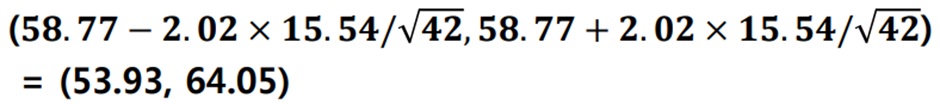
(4) 가설검정
▶ 가설검정의 절차
① 가설설정
- 귀무가설 : 현상태에 대한 잠정적 가정
- 대립가설 : 우리가 알고 싶은 것

② 검정통계량 : 귀무가설하에서 표본의 비정상성을 결정하기 위해 사용하는 통계량

③ 검정통계량의 분포와 유의수준을 비교 검토한다.

④ 결론
- 기각역 : 비정상영역 ⇒ 귀무가설 기각 ( 대립가설 채택 )
- 채택역 : 정상영역 ⇒ 귀무가설 유지 ( 대립가설 기각 )
◈ 예제 : 통계학 관련학과 취업률 ( 42개 학과 무작위 선택 )

- 해당연도의 전체 대졸 취업률은 54.5% 정도가 된다고 할 때 통계학 관련학과의 취업률 평균이 전체 취업률보다 높다고 할 수 있는가 ?
① 가설설정
- 귀무가설 : 통계학 관련학과의 취업률 평균이 전체취업률(54.5%) 보다 낮거나 같다.
- 대립가설 : 통계학 관련학과의 취업률 평균이 전체취업률(54.5%) 보다 높다.

② 검정통계량

③ 검정통계량의 분포와 유의수준을 비교
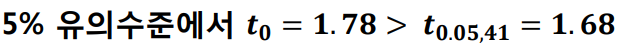
④ 결론
- 검정통계량은 기각역, 즉 비정상영역에 위치한다. 따라서 귀무가설을 기각하고 대립가설을 채택한다.
- 귀무가설이 기각되었으므로 통계학과 취업률이 전체 취업률보다 높다고 할 수 있다.
※ P-value
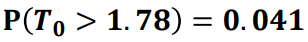
'통계학 공부' 카테고리의 다른 글
| 36. 모분산에 대한 통계적 추론 & 카이제곱분포 (0) | 2023.05.18 |
|---|---|
| 35. 모평균에 대한 통계적 추론 II (0) | 2023.05.17 |
| 33. 가설검정 (Hypothesis testing) (0) | 2023.05.15 |
| 32. 추정 (Estimation) (0) | 2023.05.14 |
| 31. 통계적 추론의 개요 (0) | 2023.05.13 |




댓글