(1) 가설검정 원리
▶ 가설검정 ( Hypothesis Testing )
- 모집단의 모수 또는 분포에 대한 추측이나 주장을 설정하고 이것의 옳고 그름을 표본의 정보를 이용하여 확률적으로 판정하는 과정을 말한다.
- 가설검정은 모집단에 대한 가설을 세우고, 이를 데이터로부터 검증하는 방법입니다.
- 가설검정은 귀무가설과 대립가설을 설정하고, 귀무가설이 기각되면 대립가설을 채택합니다.
▶ 가설(Hypothesis) : 모수 또는 분포(모집단)에 대한 추측이나 주장
- 귀무가설 (Null hypothesis): 검증하고자 하는 가설로, 보통은 모집단에 대한 기존의 믿음이나 주장을 담고 있습니다.
- 대립가설 (Alternative hypothesis): 귀무가설을 기각하게 되면 채택할 가설입니다. 대립가설은 귀무가설과 모순되는 내용을 담고 있습니다.
- 검정이란 무엇의 내용이 바르고 틀린지를 살펴보고 결정하는 일
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었다고 하자.
- 가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 한다면,
- 귀무가설 H0 μ ≥ 165
- 대립가설 H1 μ 〈 165
- 각각 가설을 설정할 수 있다.
▶ 귀무가설과 대립가설의 기본형태
- 모수 : Φ , 기존의 어떤 값 : Φ0

- 상황 ①, ②: 단측검정 ( one-sided test )
- 상황 ③ : 양측검정 ( two-sided test )
◈ 예제 : 출생성비
- 남녀의 출생성비가 다르다는 것을 보이고 싶은 경우,

◈ 예제: 취업률
- A 전공 졸업생의 취업률이 B 전공 졸업생 취업률보다 높다는 것을 보이고 싶은 경우

※ 가설검정에서 중요한 것은 첫 출발점인 가설을 잘 설정하는 것이다.
- 보이고자 하는 가설 → 대립가설
- 반대되는 가설 → 귀무가설
▶ 가설 검정의 원리
- 명제의 역, 이, 대우

- “A이면 B” 가 참(거짓)이면 그 대우도 항상 참(거짓)
귀류법은 '잘못된 것을 뒤집어서 생각해보자'라는 의미로, 논리학에서 사용되는 증명 방법 중 하나이다. 귀류법은 증명하고자 하는 명제를 부정하고, 그 부정 명제가 모순을 발생시킨다는 것을 보여서, 원래의 명제가 참임을 보이는 방법이다.
예를 들어, "모든 A는 B이다"라는 명제가 있을 때, 이를 부정하면 "어떤 A는 B가 아니다"라는 명제가 되고 이 부정 명제가 모순을 발생시킨다면, "모든 A는 B이다"는 참인 명제임을 증명할 수 있다.
귀류법은 수학적 증명이나 철학적 논의에서 많이 사용되는 방법 중 하나이다.
▶ 가설검정의 목적 : H1(대립가설)이 참 임을 보이고자 함.

⇒ 대립가설이 참 임을 밝히기가 어렵기 때문에 그 대우인 “귀무가설이 참이면 비정상적인표본이다”라는 것을 사용한다.
○ 정상과 비정상을 무엇으로 보일 것인가? ⇒ 검정통계량 (Test Statistics)
○ 어느 정도 되어야 비정상이라고 할 수 있는가? ⇒ 유의수준 (Significant Level)
★★ 가설검정의 기본원리 ★★
귀무가설하에서 표본의 비정상성여부를 통해 대립가설의 타당성을 확인하는 것이다. 이 때 사용되는 것이 검정통계량과 유의수준이다.
(2) 검정통계량과 오류
▶ 검정통계량(Test Statistic)
- 귀무가설 하에서 표본의 비정상성을 결정하기 위해 사용되는 통계량
- * 통계량 : 미지의 모수를 포함하지 않은 확률변수 → 확률분포 존재
- 통계값이 발생가능성이 희박한 위치에 있는 경우 귀무가설 기각(reject),
- 아니면 유지(retain) 또는 채택 (accept) 함.
- 검정통계량을 유도하는 방법에는 Most Powerful Test (최강력검정), Likelihood Ratio Test (가능도비 검정, LRT), Score Test 등 (수리통계학 범위) 등이 있다. 주로 점추정량을 기반으로 유도한다.
▶ 귀무가설하에서 검정통계량의 확률분포를이용하여 표본의 정상/비정상을 판정
- 기각역(rejection region) : 비정상영역 ⇒ 귀무가설 기각 ( reject )
- 채택역(acceptance region) : 정상영역 ⇒ 귀무가설 유지 ( retain / accept )
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었다고 하자.
- 가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 한다면,

◈ 예제 : 출생성비
- 남녀의 출생성비가 다르다는 것을 보이고 싶은 경우,

◈ 예제 : 취업률
- A 전공 졸업생의 취업률이 B 전공 졸업생 취업률보다 높다는 것을 보이고 싶은 경우

★★ 정상/비정상의 기준은 유의수준(significance level)으로 결정
▶ 오류의 종류

- 유의수준 : α = max P(제1종의 오류)
- β = P(제2종의 오류)
- 검정력(power) = 1- β = 1-P(제2종의 오류)
(3) 유의수준과 검정력
▶ 유의 수준(significance level)
- 통계적인 가설검정에서 사용되는 기준값이다.
- 가설검정에서 귀무가설이 맞는데도 기각하는 오류를 범할 확률을 미리 정한 값이다
- 일반적으로 유의 수준은 α로 표시하고 95%의 신뢰도를 기준으로 한다면 (1−0.95)인 0.05값이 유의수준 값이 된다.
- "유의 수준 5%란 표본을 추출해서 나온 검정 통계량이 우연히 나타날 확률 5% 미만이다."라는 뜻이다.
- 유의수준 α = max P(제1종의 오류)
◈ 예제 : 모평균의 검정
- 모집단은 N ( μ , 4 ) 일 때, μ 에 대해 μ > 0 이라는 것을 보이고자 한다.

- 귀무가설의 경계인 μ = 0 에서 P(제1종의 오류)가 최대가 되는 것을 알 수 있다.
- 따라서 유의수준 : α = 0.1587이 된다.
- 이때 귀무가설 μ < 0 을 귀무가설 μ =0 으로 표시해도 무방하다.
▶ 검정력( statistical power)
- 대립가설이 사실일 때, 이를 사실로서 결정할 확률이며, 귀무가설이 거짓일 때 이를 옳게 기각할 확률이다.
- 검정력은 알파와 반대로 베타(beta)로 표기된다.
- 검정력이 높을수록 귀무가설이 거짓임에도 불구하고 옳게 기각할 가능성이 높아지므로, 좋은 가설검정을 위해서는 높은 검정력이 필요하다.
- 검정력이 90%라고 하면, 대립가설이 사실임에도 불구하고 귀무가설을 채택할 확률(2종 오류, β error)의 확률은 10%이다.
- 검정력(power) = 1- β = 1-P(제2종의 오류 : 대립가설하에서의 귀무가설 유지)
◈ 예제 : 모평균의 검정
- 모집단은 N ( μ , 4 ) 일 때, μ 에 대해 μ > 0 이라는 것을 보이고자 한다.

- 대립가설 H1 : μ = 1 이 참이었다면,

⇒ 검정력은 크면 클수록 좋다.
▶ 유의수준 α 의 결정
- " 자료가 비정상적이다 "
- 귀무가설(H0)이 참일 때 그러한 자료를 얻을 가능성이 적어야 한다.
- 유의수준 α 의 값을 작게 설정해야 한다.
- 일반적으로 유의수준 α = 0.05 , 0.01, 0.1 등을 사용한다.
- 그 중 0.05 가 가장 많이 사용되는 유의수준이다.
- 위의 예제는 유의수준에 대하여 계산해 본 것이지만, 일반적인 경우는 먼저 유의수준을 정하고 거기에 해당하는 검정원칙(기각역)을 찾는다.
◈ 예제 : 모평균의 검정
- 모집단은 N ( μ , 4 ) 일 때, μ 에 대해 μ > 0 이라는 것을 보이고자 한다.
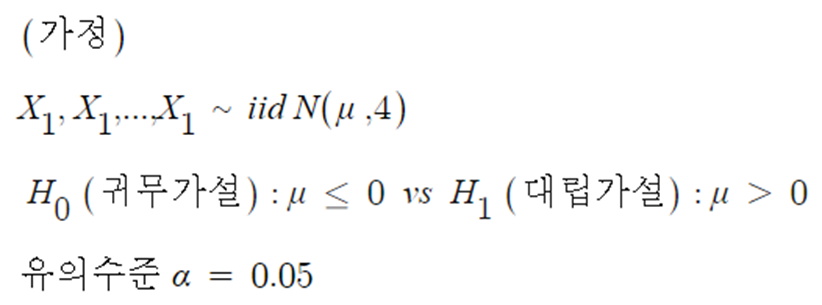
- 귀무가설(H0)의 기각역을 찾는다면,

- 대립가설 H1 : μ = 1 이 참이었다면, 제2종의 오류확률은 ?

⇒ 앞선 예제와 비교하여 기각역이 바뀌면서 귀무가설하에서의 유의수준은 낮아지고 대립가설 하에서의 제2종 오류는 증가한다.
◈ 예제 : 귀무가설 μ = 45 vs 대립가설 μ = 42

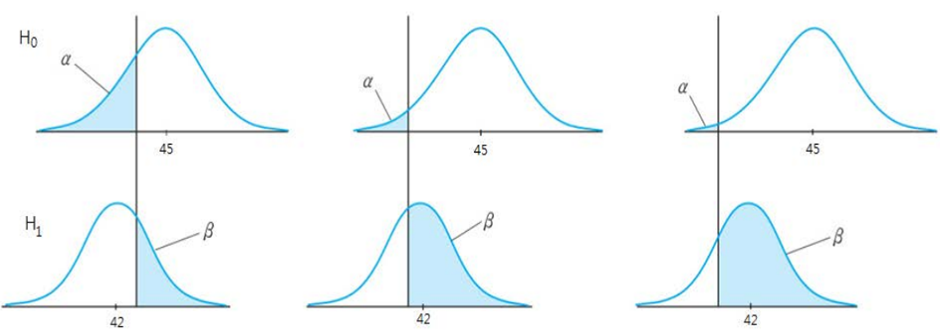
⇒ 기각역의 조정만으로 α, β 를 동시에 줄일 수 없음.
◈ 예제 : 파이 표본평균이 158 이하면 귀무가설 기각 이라 할 때,
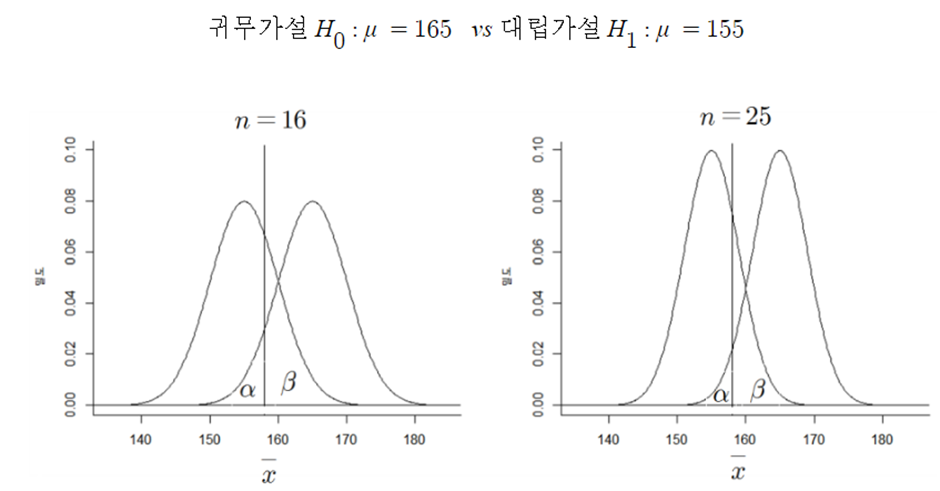
⇒ 가설검정에서 원하는 수준의 α와 β에 해당하는 표본크기(n) 결정 가능
(4) 유의확률 (P-value)
- 검정 통계량이 귀무가설을 지지하는 정도를 나타내는 확률 값이다.
- 즉, 표본 데이터에서 계산된 검정 통계량이 귀무가설을 지지하는 정도를 나타내는 값으로, 작을수록 귀무가설이 기각되기 쉽다.
- p-value는 가설검정에서 귀무가설을 기각할지 채택할지를 결정하는 기준이 되며, 미리 설정한 유의수준보다 작으면 귀무가설을 기각하고, 그렇지 않으면 귀무가설을 채택한다.
- 일반적으로 유의수준은 0.05 혹은 0.01이 사용되며, 이 값보다 작은 p-value를 가지면 귀무가설을 기각한다.
- p-value < α ⇒ 귀무가설 기각, p-value > α ⇒ 귀무가설 유지
▶ 유의 수준과 유의 확률의 비교
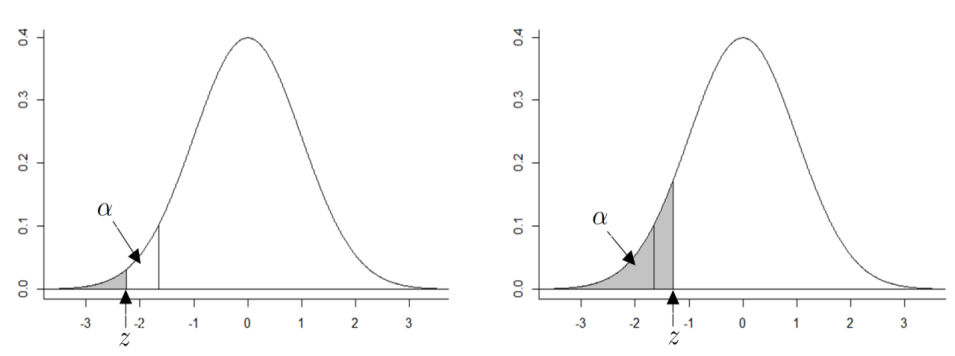
○ 유의확률은 확률분포와 확률분포의 표본값 1개가 주어졌을 때 그 확률분포에서 해당 표본값 혹은 더 희귀한(rare) 값이 나올 수 있는 확률로 정의한다.
○ 관측값에 의해 귀무가설을 기각시킬 수 있는 최소 유의 수준
- p-값 < α → 귀무가설 기각
- p-값 > α → 귀무가설 유지
◈ 예제 : 기존 파이의 평균 칼로리는 165kcal 이었다고 하자.
- 가설검정을 통해 새로운 파이는 기존의 파이보다 칼로리가 낮다는 것을 보이고자 한다면,

- 관측값 평균이 156 kcal 이었다면,

⇒ 결론 : 5% 유의수준에서 새로운 파이의 평균 칼로리는 기존 파이의 칼로리보다 낮다고 할 수 있다.
- 이 때, 유의확률 (P-값)을 구하면,
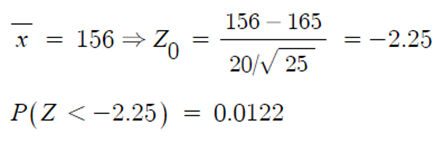
⇒ p-값 0.0122 < 유의수준 α 0.05 이므로 귀무가설 기각
- 결론 : 5% 유의수준에서 새로운 파이의 평균칼로리는 기존 파이의 칼로리보다 낮다고 할 수 있다.
'통계학 공부' 카테고리의 다른 글
| 35. 모평균에 대한 통계적 추론 II (0) | 2023.05.17 |
|---|---|
| 34. 모평균에 대한 통계적 추론 & T분포 (1) | 2023.05.16 |
| 32. 추정 (Estimation) (0) | 2023.05.14 |
| 31. 통계적 추론의 개요 (0) | 2023.05.13 |
| 30. 이항분포의 정규근사 (1) | 2023.05.12 |




댓글