- 추정은 표본을 통해 모집단의 모수를 추측하는 것을 의미한다.
- 추정은 표본의 정보를 활용하여 모집단에 대한 정보를 얻는 데에 중요한 역할을 한다.
- 추정은 점추정과 구간추정으로 나눌 수 있다.
- 점추정은 하나의 값으로 모수를 추정하는 것을 의미하며, 대표적으로 표본평균이나 표본분산 등이 있다.
- 구간추정은 추정값이 포함될 수 있는 구간을 계산하여 모수를 추정하는 것을 의미한다.
(1) 점추정(Point Estimation)
- 점추정은 하나의 값으로 모수를 추정하는 것을 의미한다.
- 점추정량을 계산하는 방법에는 여러 가지가 있지만, 대표적인 방법으로 적률법, 최대가능도추정법, 최소제곱법이 있다.
▶ 적률법(Method of Moments)
- 적률법은 추정하려는 모수에 대한 표본 적률을 모수의 적률로 대입하여 추정하는 방법이다.
- 이 방법은 모수의 적률을 통해 모집단 분포의 특성을 추정한다.
- 예를 들어, 모집단의 평균을 추정하려면 표본의 평균을 사용하고, 모집단 분산을 추정하려면 표본 분산을 사용한다. 이러한 방법은 모수 추정에 대한 직관적인 이해를 제공한다.
◈ 예시 : 확률분포에서 모수는 기대값으로 표시


- 위 표본의 기대값으로 아래와 같이 모집단의 평균과 분산을 추정할 수 있다.

▶ 최대가능도추정법 (Maximum Likelihood Estimation, MLE)
- 최대가능도추정법은 관측된 데이터를 바탕으로 모집단 분포의 모수를 추정하는 방법이다.
- 이 방법은 주어진 데이터에서 가능도 함수를 최대화하는 모수 값을 찾는다.
- 가능도 함수는 모수를 알 때 주어진 데이터가 나타날 확률을 나타낸다.
- 이 방법은 대규모 표본에서 일반적으로 잘 작동하지만, 작은 표본에서는 부정확할 수 있다.
▷ 가능도(Likelihood, 우도) 함수
- 확률 분포의 모수가, 어떤 확률변수의 표집값과 일관되는 정도를 나타내는 값이다.
- 구체적으로, 주어진 표집값에 대한 모수의 가능도는 이 모수를 따르는 분포가 주어진 관측값에 대하여 부여하는 확률이다.
◈ 예시 : 아래와 같은 이항분포
- 만약 성공할 확률을 모르고 있을 때 8이 관측되었다면, 8이라는 자료를 얻을 가능성은 ?



- 최대 높이의 위치 → 최대 가능도 추정량 (MLE)
▷베이지안 추론

- 사후분포는 사전분포에 가능도함수를 곱한 값이라 할 수 있다.
▶최소제곱법 (Least Squares Estimation)
- 최소제곱법은 회귀분석에서 사용되는 방법으로, 표본의 관측값과 모델의 예측값 간의 잔차제곱합을 최소화하는 모수 값을 추정하는 방법이다.
- 예를 들어, 선형회귀에서는 최소제곱법을 사용하여 최적의 회귀선을 찾는다.
- 이 방법은 데이터의 분포에 대한 가정이 필요하고, 이상치에 민감할 수 있다.
▶ 직관적인 추정량
- 위와 같은 방법을 통해서 점추정량을 계산할 수 있음.
- 그러나 분포가 복잡하면 값을 구하기가 상당히 어려움. 따라서 직관적인 추정량을 사용한다.
▷ 모수 ← 통계량 (직관적인 추정량)
- 모평균 ← 표본평균
- 모비율 ← 표본비율
- 모분산 ← 표본분산
- 모표준편차 ← 표본표준편차
- 추정량(estimator)은 확률변수, 추정치(estimate)는 실제관측값
- 점추정량이 정확히 모수와 일치할 가능성은 거의 없다. ( 대부분 연속변수이기 때문에 )
※ 구간추정과 가설검정에서 점추정량은 기준통계량으로 사용한다.
▶ 좋은 추정량의 요건
▷일치성(consistency)
- 표본의 크기가 커질수록 추정량이 모수에 근사해야 합니다. 이를 일치성이 있다고 합니다. (대수의 법칙)
- 예를 들어, 표본의 평균이 모평균을 추정하는 추정량인 경우, 표본의 크기가 커질수록 표본평균은 모평균에 점점 가까워집니다.
- 이렇게 추정량이 모수에 근사해가는 것을 일치성이 있다고 합니다.

▷ 비편향성(unbiasedness, 불편성)
- 추정량의 기댓값이 모수와 같아야 합니다. 이를 비편향성이 있다고 합니다.
- 예를 들어, 표본의 평균이 모평균을 추정하는 추정량인 경우, 표본평균의 기댓값은 모평균과 같습니다.
- 이렇게 추정량의 기댓값이 모수와 같은 것을 비편향성이 있다고 합니다.
- 편향(편의) : 기대값과 모수의 차이


- 비편향 추정량 : 기대값과 모수의 차이가 없을 때

◈ 예시
- 평균의 기대값은 모수(모평균)과 같기 때문에 비편향이다.

- 표준편차는 편향(편의) 추정량 (biased estimator)

※ 표준편차가 편향을 보이긴 하지만 편향의 정도가 미미하고, 위 일치성을 만족하여 크게 편향에 대한 영향이 없어 그대로 사용한다.

▷효율성
- 추정량의 분산이 작을수록 좋습니다. 이를 효율성이 있다고 합니다.
- 예를 들어, 분산이 작은 추정량은 다른 추정량보다 표본의 크기가 크지 않은 경우에도 추정값이 더 가까이 모수에 있을 가능성이 큽니다.
- 이렇게 추정량의 분산이 작은 것을 효율성이 있다고 합니다.
- 추정량을 비교하는 측도 : MSE(Mean Square Error)

※ MSE는 분산과 bias 제곱의 합으로 표현되며, 작을수록 더 효율적이다.
(2) 구간추정(Interval estimation)
- 구간추정은 표본에서 계산한 통계량(예: 표본평균)을 이용하여 모수(예: 모평균)가 속할 가능성이 높은 구간을 추정하는 방법이다.
- 일반적으로, 구간추정은 표본으로부터 계산된 점추정치(예: 표본평균)와 구간추정의 신뢰도를 나타내는 신뢰수준(예: 95%)을 이용하여 구간을 추정한다.
- 미지의 모수가 포함될 것으로 기대하는 범위를 확률적으로 택하는 과정이다.
▷ 신뢰구간 (confidence interval, CI )
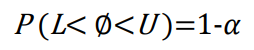
- L과 U는 확률변수로 이를 유도하는 데 점추정량이 중심적 역할을 함.
- 100(1-α)%를 신뢰수준(confidence level)이라 부른다.
- 신뢰구간(CI)에 모집단 실제 평균값이 포함될 확률을 '신뢰구간의 신뢰수준(Confidence Level)'이라함.
- 일반적으로 95% 신뢰수준에서의 신뢰구간을 사용한다.
◈ 예시 : 모평균 에 대한 95% 신뢰구간

- 점추정량 X의 통계적 성질
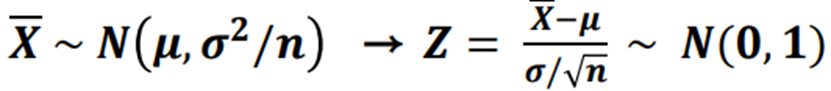
⇒ Z : 모수와 통계량으로 이루어져 있고 분포는 미지모수를 포함하지 않음.
★ 중심축량(pivotal quantity, 주축량) - 신뢰구간 계산의 중심임.
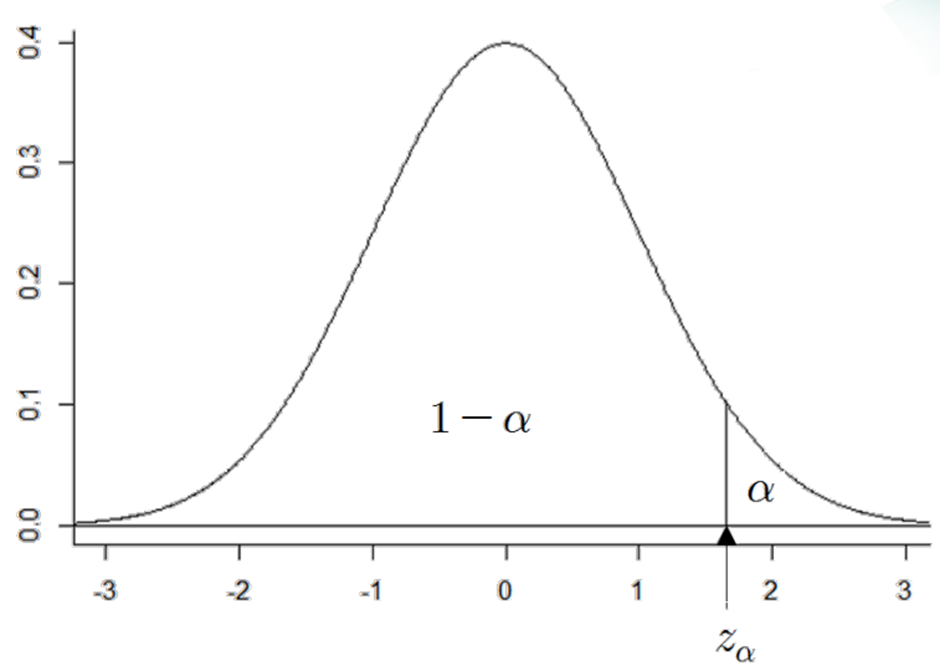
○ 표준 정규분포로부터 0.95를 가지는 Z 값을 이용하여 구간을 구한다.
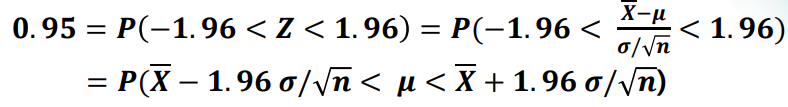
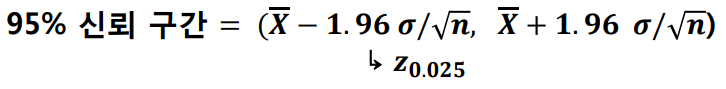
○ 95% 신뢰구간에서 -1.96과 1.96 대신 확률을 만족시키는 다른 값을 사용할 수 있는가?
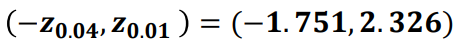
⇒ 95%의 신뢰구간이지만 위의 1.96 대비 비효율적이다. 더 넓은 편차를 가지고 있기 때문에 최소편차인 +/- 1.96을 95% 신뢰구간으로 사용한다.
○ 단측신뢰구간 (one-sided CI)
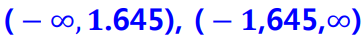
◈ 예제 : 파이에 포함된 칼로리의 모평균
- 파이의 칼로리는 표준편차가 8인 정규분포를 따른다고 가정
- 16개의 파이를 무작위로 조사
- 16개의 파이의 표본평균(kcal)이 162.7
- 모평균의 95% 신뢰구간은 ?
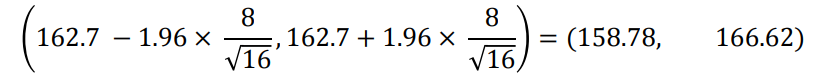
○ 위의 구간 (158.78,166.62) 사이에 모평균이 있을 확률은 0.95인가 ?
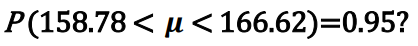
- 빈도론자(frequentist) 관점에서 ⇒ 아니다. 추출된 평균( μ) 은 상수이기 때문에 확률은 1 이된다.
- 베이지안 추론 관점에서 ⇒ 어느 정도 가능하다.
- 추출된 평균( μ) 은 확률변수이고 credible interval ( 신용구간, 신뢰구간 )으로 해석한다.
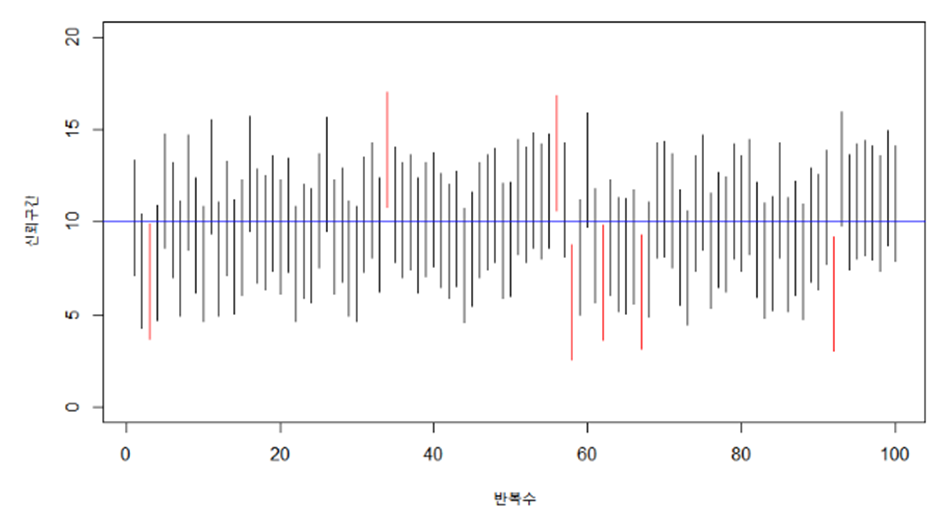
▶ 빈도론자(frequentist) 관점

⇒ n번의 시행 중에 95%에는 신뢰구간안에 μ 가 포함되어 있다는 것이다.
'통계학 공부' 카테고리의 다른 글
| 34. 모평균에 대한 통계적 추론 & T분포 (1) | 2023.05.16 |
|---|---|
| 33. 가설검정 (Hypothesis testing) (0) | 2023.05.15 |
| 31. 통계적 추론의 개요 (0) | 2023.05.13 |
| 30. 이항분포의 정규근사 (1) | 2023.05.12 |
| 29. 표집분포, 대수의 법칙, 중심극한정리 (0) | 2023.05.11 |




댓글