모집단의 모수를 알 수 없기 때문에 이론적으로 표본에서 추출한 모든 표본에 대해 통계량을 계산할 수는 없다. 따라서, 표본에서 얻은 통계량이나 검정통계량 등이 어느 정도의 변동성을 가지는지에 대한 정보를 이용하여 추론을 하게 된다. 이 때, 표본에서 얻은 통계량의 분포를 표집분포(sampling distribution)라고 부르며, 표집분포를 이용하여 통계적 추론을 수행한다.
(1) 이항분포의 정규근사
- 이항분포는 대표적인 이산형 확률분포이지만, 표본 크기가 충분히 크고 확률 파라미터 값이 적당한 경우에는 정규분포로 근사할 수 있다.
- 이러한 근사를 사용하면, 이항분포를 다루기 어려운 경우에도 정규분포의 성질을 활용하여 다양한 추론을 수행할 수 있다.
- 특히, 정규분포의 선형성과 대칭성, 표준화 등의 성질을 이용하면 이항분포에 대한 확률 계산이 간단하고 직관적으로 이루어집니다. 이러한 이유로, 이항분포의 정규근사는 통계적 추론에서 매우 중요한 역할을 한다.
▶ 이항분포의 근사
X ~ B ( n, p ) 인 이항분포에서 n이 클 때,
- p 가 작은 경우 → 포아송 근사
- p가 큰 경우 → 포아송 근사
- p가 0.5에서 많이 벗어나지 않는 경우 → 정규근사
◈ 예제 : X ~ B ( 100, 0.4 ), E(X) = 40 일때,
- 이항분포
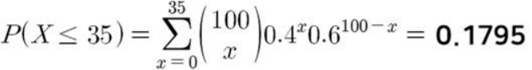
- 포아송 근사
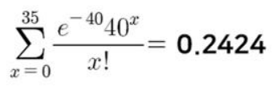
⇒ p 가 0.5 근처라 포아송 근사가 적합하지 않다.
▶ 이항분포 기대값과 분산 : X ~ B ( n, p )

▶ n이 큰 경우 중심극한정리에 의해, 표본평균값의 분포는 정규분포에 가까와진다.

▶ 위 식을 표준화하면,
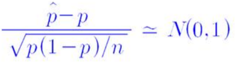
▶ 표준화된 식의 분자,분모에 n을 곱해 정리하면,
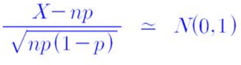
▶ 위 식은 아래 식으로 표현할 수 있다.
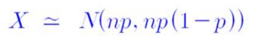
⇒ 즉, X는 정규분포에 근사한다는 것을 보여준다.
▶ X ~ B ( 100, 0.04 ) 와 X ~ B ( 100, 0.4 ) 의 분포
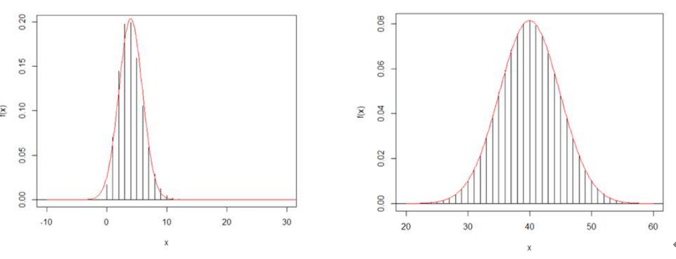
⇒ p가 0.5에 가까울 때 정규근사가 더 잘된다.
(2) 연속성 수정 (Continuty Correction)
- 이항분포의 정규근사에서 연속성 수정(continuity correction)은 이항분포의 확률을 정규분포로 근사하는 경우 발생하는 근사 오차를 보정하기 위한 방법이다.
- 이항분포는 이산형 확률분포로, 특정한 확률 변수가 가질 수 있는 값들이 이산적이다.
- 반면에 정규분포는 연속형 확률분포로, 특정한 확률 변수가 가질 수 있는 값들이 연속적이다.
- 이러한 차이 때문에 이항분포의 확률을 정규분포로 근사화할 때, 근사 오차가 발생한다.
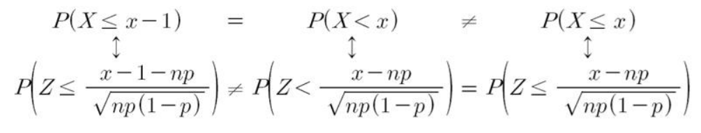
▶ 연속성 수정

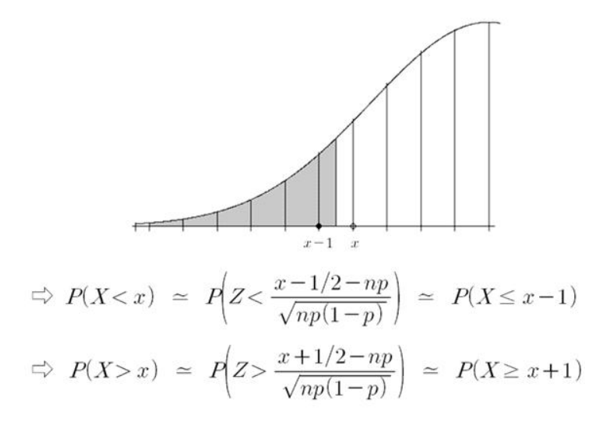
⇒ 이항분포 x 값에서 1/2 만큼 더하거나 빼서 수정한다.
◈ 예제 : 여론조사
- 전체국민 60%가 A 정책에 대해 찬성한다고 주장
▶ 150명을 무작위로 뽑아 찬성하는 사람의 비율을 알아보려고 할 때, 적극찬성하는 사람이 78명 이하일 확률은 ?
- X ~ B ( 150, 0.6 ) 일 때 P(X≤78) ?
- 이항분포 가정하에서의 정확한 확률 = 0.0284
- 정규분포 근사로 풀면,
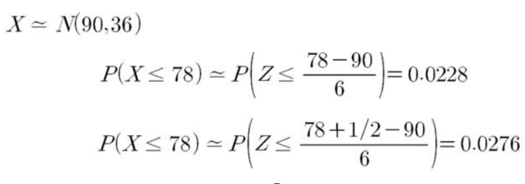
⇒ 연속성 수정을 했을 때 정확한 확률에 더 근접하다.
'통계학 공부' 카테고리의 다른 글
| 32. 추정 (Estimation) (0) | 2023.05.14 |
|---|---|
| 31. 통계적 추론의 개요 (0) | 2023.05.13 |
| 29. 표집분포, 대수의 법칙, 중심극한정리 (0) | 2023.05.11 |
| 28. 확률표본과 통계량 그리고 표집분포 (0) | 2023.05.10 |
| 27. 연속확률분포 - 정규분포 (Normal Distribution) (0) | 2023.05.09 |




댓글