모집단의 모수를 알 수 없기 때문에 이론적으로 표본에서 추출한 모든 표본에 대해 통계량을 계산할 수는 없다. 따라서, 표본에서 얻은 통계량이나 검정통계량 등이 어느 정도의 변동성을 가지는지에 대한 정보를 이용하여 추론을 하게 된다. 이 때, 표본에서 얻은 통계량의 분포를 표집분포(sampling distribution)라고 부르며, 표집분포를 이용하여 통계적 추론을 수행한다.
(1) 표집분포 (sampling distribution)
▶ 표집분포는 통계량의 확률분포이다.
▶ 통계량은 측정가능한 확률표본의 함수이다.
▶ 관심통계량
- 표본평균(표본비율)
- 표본분산, 표본표준편차,
- 극한값 : 최대값 - 최소값 → 범위
- 순위 (rank)
이런 통계량들이 모수와 연관되어 있기 때문에 이들에 대해 아는 것이 중요하다.
(2) 표본평균의 성질
◈ 예제 : 확률분포가 다음과 같을 때

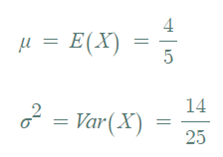
▶ 두 개의 확률표본을 추출한 경우, 두 표본의 평균의 분포는 ?





- 표준오차(standard error, SE ) : 통계량으로 이루어진 모집단의 표준편차
⇒ 평균의 표준오차란 표본 평균 분포의 표준편차
▶ 표본평균의 분포는 어떻게 바뀔까 ?
- 위 예제에서 확률분포는

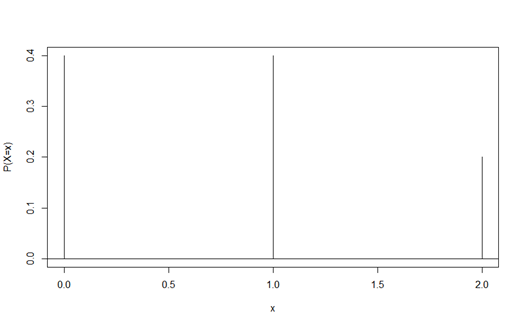
- 두 개의 확률표본을 추출한 경우, 두 표본의 평균의 분포는

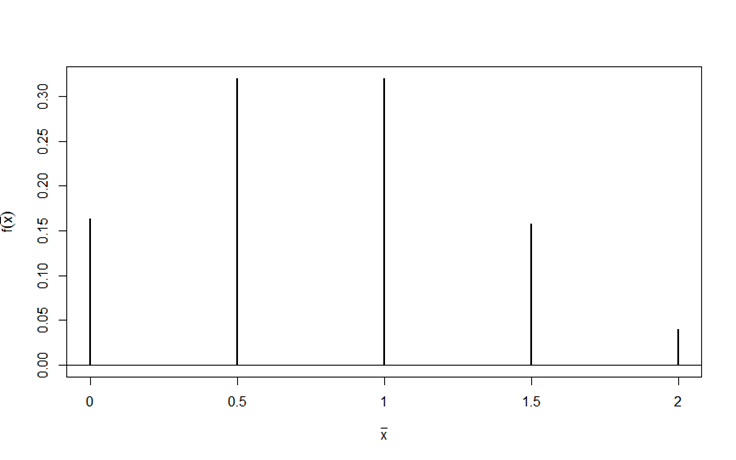
- 이렇게 바뀌었다. ⇒ 일반적인 형태에서는 이 분포가 다양하게 바뀔 수 있다.
▶ 모집단이 정규분포라면,
- 두 정규확률변수의 선형결합도 정규분포를 따름
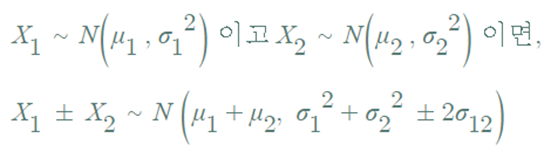
- 추가 가정 : 두 정규확률변수가 독립이면, 공분산이 0 이므로,
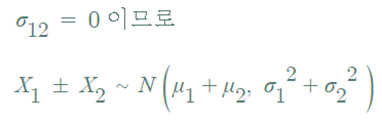
- 정규분포에서 확률표본을 추출한다면,

- 각각의 확률표본의 합의 분포는,

- 표본평균의 분포는,

※ 확률을 구하기 위해서는 표준화가 필요하다.

⇒ 정규 확률 표본의 표본 평균의 분포는 정규분포이다.
▶ 모집단이 정규분포가 아닌 경우,

▶ 다른 분포는 ?
- 직접유도
- 근사분포 유도
- Monte Carlo 모의실험을 통해 표집분포 추정
(3) 대수의 법칙 ( law of large numbers )
- 대수의 법칙 혹은 큰 수의 법칙은 확률표본의 표본평균은 표본크기가 커지면 모평균에 수렴한다라는 것이다.

- 이 때, n을 계속 크게 만들면

(4) 중심극한정리 ( Central Limit Theorem : CLT )
- 중심극한정리는 모집단에서 취한 표본 평균값의 분포는 표본 수가 커질수록 평균값을 중심으로 하는 정규분포에 가까워진다는 정리이다.
- 즉, 확률표본의 표본평균은 표본크기가 커지면 정규분포에 근사한다.

◈ 예제 : 확률분포가 다음과 같을 때
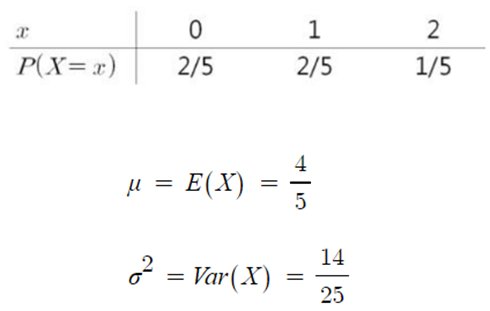
- 확률표본 50개를 뽑아 더한 값의 분포는 ?

⇒ n이 커질수록 모집단의 형태와 관계없이 정규분포에 근사한다.

'통계학 공부' 카테고리의 다른 글
| 31. 통계적 추론의 개요 (0) | 2023.05.13 |
|---|---|
| 30. 이항분포의 정규근사 (1) | 2023.05.12 |
| 28. 확률표본과 통계량 그리고 표집분포 (0) | 2023.05.10 |
| 27. 연속확률분포 - 정규분포 (Normal Distribution) (0) | 2023.05.09 |
| 26. 이산확률분포 - 다항분포 (Multinomial Distribution) (0) | 2023.05.08 |




댓글