통계학 관점에서 표본을 뽑는 이유는 ?
⇒ 모집단에 대한 추론을 하기 위해서이다.
추론은 통계학의 핵심이다. 추론을 통하여 표본에서의 값을 일반적인(모집단) 경우로 확대 적용하는 것이다.
(1) 확률표본( Random sample )
- 확률표본(random sample)은 모집단에서 무작위로 추출한 표본으로, 각각의 표본은 동일한 확률로 추출된다는 특징을 가지고 있다. 이를 통해 표본이 모집단을 대표하고 있다고 가정할 수 있으며, 통계적 추론을 할 때 이를 이용하여 모집단의 특성을 추정하거나 가설 검정을 수행한다.
- 즉, 확률표본은 통계적 추론의 첫걸음이다.
- 확률표본은 모집단에서 추출한 표본으로, 이를 통해 확률분포를 추정할 수 있다. 확률분포는 확률표본으로부터 구한 통계량의 분포를 의미한다.
- 예를 들어, 키에 대한 모집단 분포를 추정하기 위해 무작위로 표본을 추출할 때, 이를 통해 추정한 통계량인 평균과 표준편차를 이용하여 정규분포를 추정할 수 있다. 이러한 정규분포는 확률표본에서 얻은 통계량을 중심으로 분포하게 된다.
- 따라서, 확률표본과 확률분포는 서로 밀접한 관련이 있으며, 확률표본에서 추출한 통계량을 이용하여 확률분포를 추정할 수 있다.
- 확률분포를 통해 확률변수가 어떤 값을 취할 확률을 구할 수 있고, 확률표본은 확률분포에서 추출한 하나의 값으로, 확률분포를 통해 어떤 값이 추출될 확률을 구할 수 있다.
▶ 확률표본 추출
- 확률표본은 확률을 통계량으로 바꾸는 단계에 필요한 부분이다.
- 확률표본은 모집단에서 무작위로 선택되어진 관측값을 말한다.
- 확률표본이 만족해야 할 요소는 서로 독립이고 동일한 분포를 따른다고 가정한다. (independent and identically distributed - iid )
- 정규분포에서 확률표본을 추출한 경우 아래와 같이 표현한다.

▶ 확률표본의 성질
- 독립이기 때문에 결합분포는 각각의 주변분포 곱으로 표시

- 동일한 분포이기 따르기 때문에 동일한 확률질량(밀도)함수를 가짐

- X1,...,Xn 이 확률표본이고, Xi ~ f(x) 이면, 결합분포는,
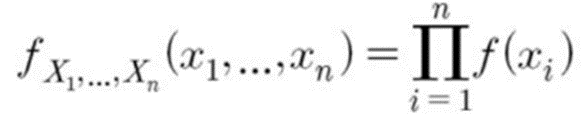
◈ 예제 : 윷놀이
- 윷이 젖혀지면 1, 업어지면 0 이라 한다고 할 때, 4번 던졌을 때, 이 확률분포의 결합확률질량함수는?

(2) 통계량(Statistics)
- 확률분포로부터 추출된 확률표본에 대해 계산 가능한 함수를 통계량(statistic)이라고 한다.
- 통계량은 데이터의 특성을 요약하거나 추정하는 데 사용되며, 확률분포를 이용하여 계산된다.
- 예를 들어, 평균, 분산, 상관계수, 회귀계수 등이 대표적인 통계량이다.
- 통계량은 관측가능한 표본의 함수를 말한다. 관측가능하다는 것은 미지의 모수를 포함하지 않음을 의미하며, 모수란 모집단의 수치적 특성을 말한다.
◈ 예제 : 모수와 통계량
- 전교생이 20,000명인 어느 대학교 학생들의 평균 키를 알아보려고 한다.
- 전교생 20,000명 모두 키를 재고 평균을 내면 모수.
- 10명의 학생을 뽑아 키를 재고 평균을 내면 통계량
※ 10명의 학생의 키 평균이 170 cm라 했을 때, 새롭게 10명을 뽑아 키 평균을 내면 170cm를 기대할 수 없다.
▶ 추정량과 추정치(추정값)
- 확률표본에서 얻은 데이터를 이용하여 모수에 대한 정보를 추정하고자 할 때, 그 추정에 사용되는 통계량을 추정량(estimator)이라고 한다.
- 추정량은 확률표본으로부터 계산되는 함수로 정의되며, 추정량을 이용하여 모수에 대한 추정치(estimated value)를 계산할 수 있다.
- 추정량은 모수를 추정하기 위해 사용하는 공식이나 방법론이며, 추정치는 해당 공식이나 방법론을 적용하여 계산된 값이다.
- 예를 들어, 확률표본의 평균을 이용하여 모평균을 추정할 경우, 평균은 추정량이 되고, 그 추정량에 확률분포에서 계산된 신뢰구간이나 신뢰도 등을 반영하여 구한 값이 추정치가 된다.
- 추정치는 추정량에 따라 달라지게 되며, 추정량을 통해 구한 추정치의 정확성과 신뢰성을 검증할 수 있다.
- 추정량(estimator) : 모수의 추정에 사용되는 통계량
- 추정치(estimated value : 추정값) : 추정량의 관측값
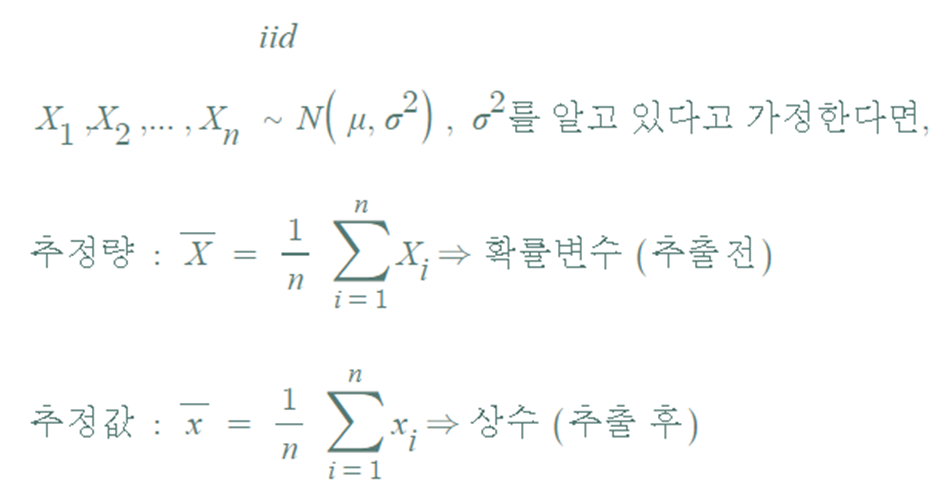
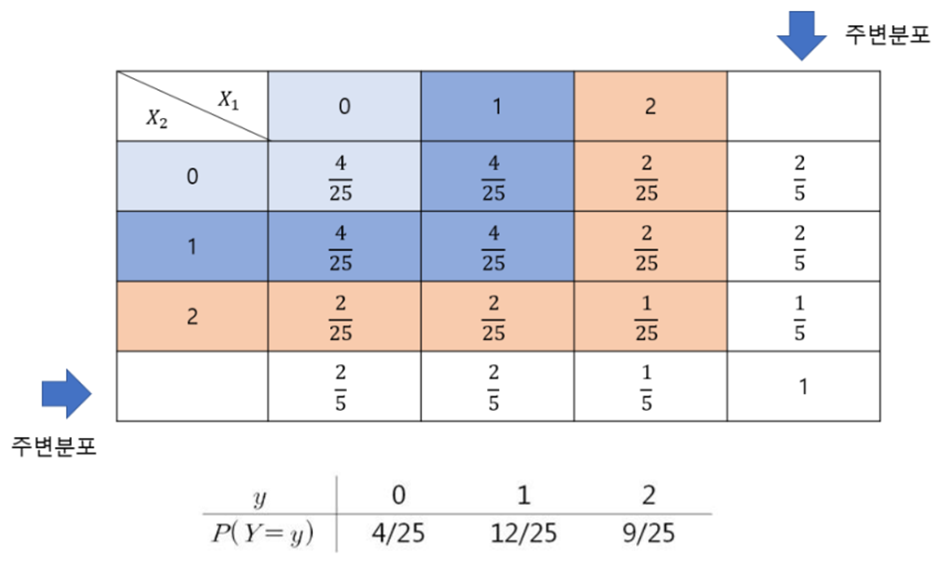
◈ 예제 : 확률분포가 다음과 같을 때,

- 두 개의 확률표본 X1, X2 를 추출하여, 두 확률표본 중 최대값의 나타내는 함수의 분포는?
- 즉, Y = max(X1, X2)일 때 Y의 분포를 찾는 것.
- 위 분포는 결합분포를 나타내고 서로 독립이다.

(3) 표집분포 ( Sampling distribution )
- 표집분포는 통계량의 (모집단) 확률분포이다.
- 통계량의 값은 표본 추출 때마다 바뀌게 된다. 즉 통계량은 확률변수가 된다. 확률분포는 확률변수가 특정값을 가질 확률을 말한다.
- n개의 크기를 가지는 표본을 모집단에서 반복해서 추출하여 나온 통계량의 확률분포가 표집분포이다. 결국 표집분포는 모집단의 확률분포를 나타낸다.
▶ 표집분포를 구하는 법
- 모든 가능한 표본의 경우를 나열한다.
- 각 표본에 대하여 통계량의 값을 계산한다.
- 얻어진 통계량의 값 중에서 서로 다른 값을 나열하고, 같은 값을 가지는 통계량의 개수를 세어 확률을 정한다.
▶ 표집분포를 사용하는 이유
- 표본에서 얻은 정보를 이용하여 모집단에 대한 추론을 하기 위해서는 표본에서 얻은 통계량을 이용하여 모집단의 모수를 추정하거나, 두 개 이상의 모집단 간의 차이를 비교하는 등의 통계적 가설검정을 수행해야 한다. 이 때, 표본에서 얻은 통계량이나 검정통계량 등이 얼마나 변동성을 가지는지를 알아야 한다.
- 하지만 모집단의 모수를 알 수 없기 때문에 이론적으로 표본에서 추출한 모든 표본에 대해 통계량을 계산할 수는 없다. 따라서, 표본에서 얻은 통계량이나 검정통계량 등이 어느 정도의 변동성을 가지는지에 대한 정보를 이용하여 추론을 하게 된다. 이 때, 표본에서 얻은 통계량의 분포를 표집분포(sampling distribution)라고 부르며, 표집분포를 이용하여 통계적 추론을 수행한다.
- 즉, 표집분포는 모집단에서 표본을 추출하는 과정에서 생기는 불확실성을 반영하여, 표본에서 얻은 통계량이 모집단에서 어떤 값을 가질 확률분포를 의미한다. 이를 이용하여 추론을 하면, 표본에서 얻은 통계량의 신뢰성이나 유의성 등을 평가할 수 있다. 따라서, 표집분포를 활용하는 것은 통계적 추론에 있어서 꼭 필요한 부분이다.
'통계학 공부' 카테고리의 다른 글
| 30. 이항분포의 정규근사 (1) | 2023.05.12 |
|---|---|
| 29. 표집분포, 대수의 법칙, 중심극한정리 (0) | 2023.05.11 |
| 27. 연속확률분포 - 정규분포 (Normal Distribution) (0) | 2023.05.09 |
| 26. 이산확률분포 - 다항분포 (Multinomial Distribution) (0) | 2023.05.08 |
| 25. 이산확률분포 - 기하분포 & 음이항분포 (0) | 2023.05.07 |




댓글