확률분포의 분류
▷ 이산확률분포 : 베르누이 분포, 이항분포, 초기하분포, 포아송분포, 기하분포, 음이항분포, 다항분포 등
▷ 연속확률분포 : 정규분포, t 분포, 카이제곱분포, F 분포 등
(1) 정규분포 ( Normal Distribution )
▶ 통계학 분야에서 가장 중요한 분포
▶ 정규분포의 확률밀도함수
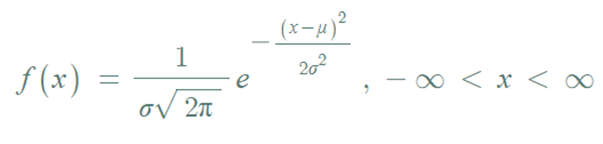
▶ 가우스 ( C.F Guass )
- 가우스(Gauss) 또는 카를 프리드리히 가우스(Carl Friedrich Gauss)는 18세기 말부터 19세기 초에 걸쳐 살았던 독일의 수학자, 천문학자, 물리학자, 통계학자, 지리학자이다. 그의 이름은 통계학에서도 잘 알려져 있다.
- 가우스는 통계학 분야에서는 최소제곱법과 정규분포를 중심으로 한 연구를 했다. 최소제곱법은 특정한 데이터 셋과 가장 근접한 직선을 찾는 방법으로, 데이터 분석에서 매우 중요한 개념 중 하나이다.
- 또한 가우스는 정규분포를 발견하였으며, 이 분포는 통계학에서 가장 중요한 분포 중 하나이다. 정규분포는 대부분의 데이터 분포를 설명하는데 유용하게 사용되며, 중심극한정리의 기반이 되는 분포이기도 하다.
- 1809 최소제곱법 (method of least squares)의 개념 소개
- 위치모수의 추정값으로 산출평균이 적절함(오차의 정규법칙)을 보이는 과정에서 정규분포의 밀도함수 형태를 유도
▶ 피어슨 ( K. Pearson )
- 정규분포는 18세기 말에 카를 프리드리히 가우스(Carl Friedrich Gauss)가 발견하였고, 이후에 피어슨(William Sealy Gosset)과 피셔(Ronald A. Fisher) 등에 의해 널리 사용되었다.
- 피어슨은 정규분포를 확률분포로서 첫 번째로 본격적으로 사용한 사람 중 한 명이다.
- 어떤 사건이 정규분포를 따른다면, 평균과 분산을 알면 그 사건이 어떤 범위 내에 속할 확률을 구할 수 있다
- normal (정규분포) 본격적으로 사용 ( 표준편차 σ )
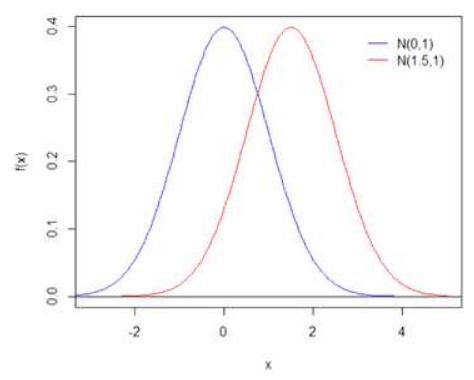
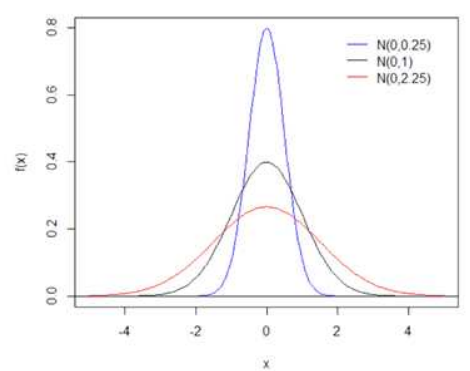
▶ 정규분포의 표현


▶ 확률계산 P( a < X < b ) = ?

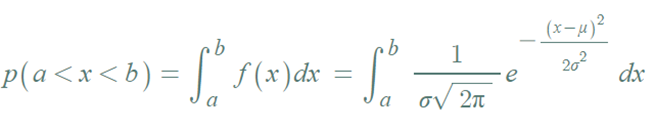
(2) 표준 정규 분포 (Standard normal distribution)
- 표준정규분포(Standard Normal Distribution)는 평균이 0이고 분산이 1인 정규분포를 말한다.
- 이 분포는 다른 정규분포를 표준화(standardize)하는 데 사용한다.
- 표준화란 어떤 분포의 값을 평균으로부터 얼마나 떨어져 있는지를 나타내는 표준편차의 개념으로 변환하는 것이다.
- 표준화를 통해 서로 다른 평균과 분산을 가지는 여러 정규분포를 표준적인 비교가 가능하고, 이를 이용해 다른 확률분포와의 연관성을 파악하는 등 다양한 분석에 활용할 수 있다.
- 표준정규분포의 확률값은 표준정규분포표에서 직접 확인할 수 있으며, 이를 이용해 확률값을 추정하는 데에도 활용된다.
▶ 표준정규분포의 확률밀도함수

- 일반적으로 Z 로 표시. Z ~ N( 0 , 1 )
▶ 확률 계산
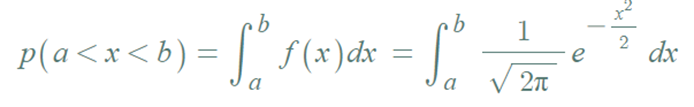
- 위 식을 이용하여 수치 해석학적으로 계산할 수 있다.
- 그러나, 계산이 어렵기 때문에 주로 표준정규분포표를 이용하여 확률계산을 한다.
- 요즘은 R, python 등 통계프로그램을 이용하여 계산한다.
표준정규분포표
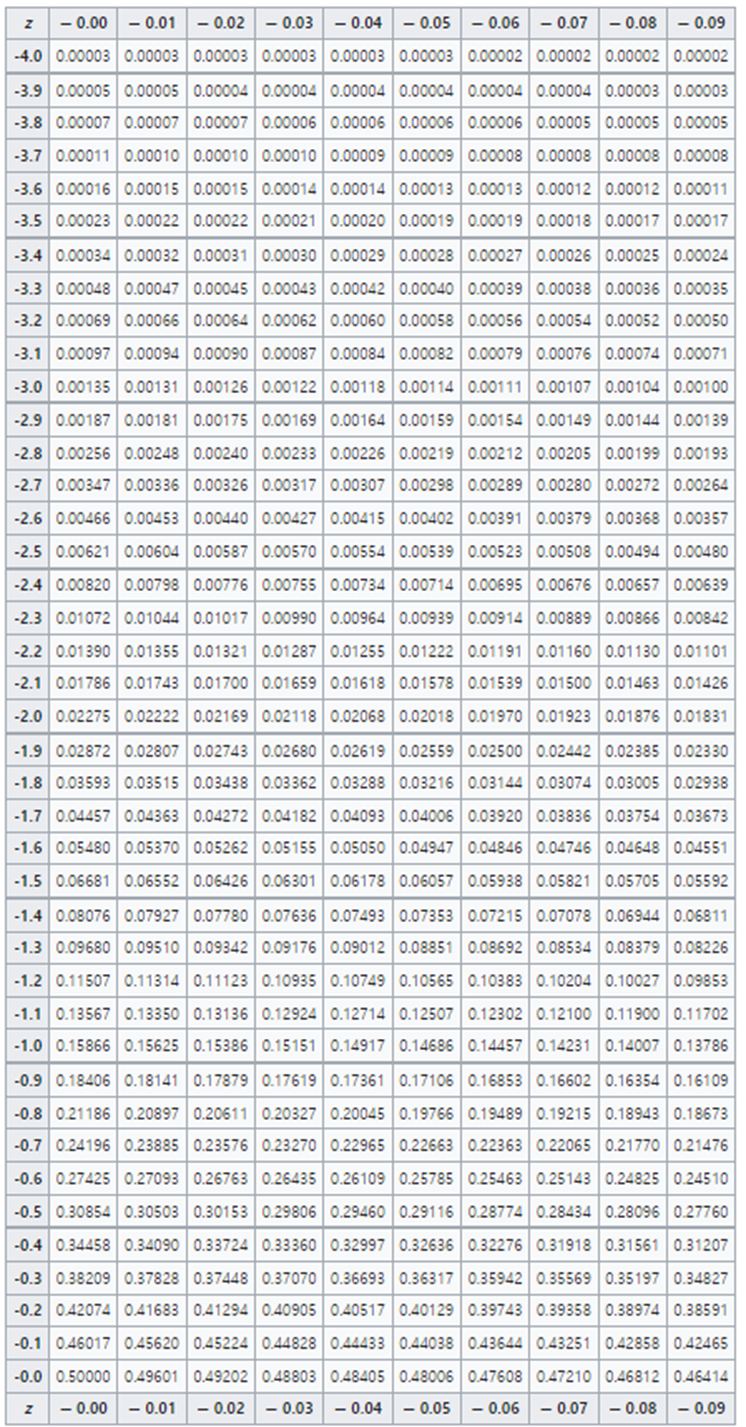
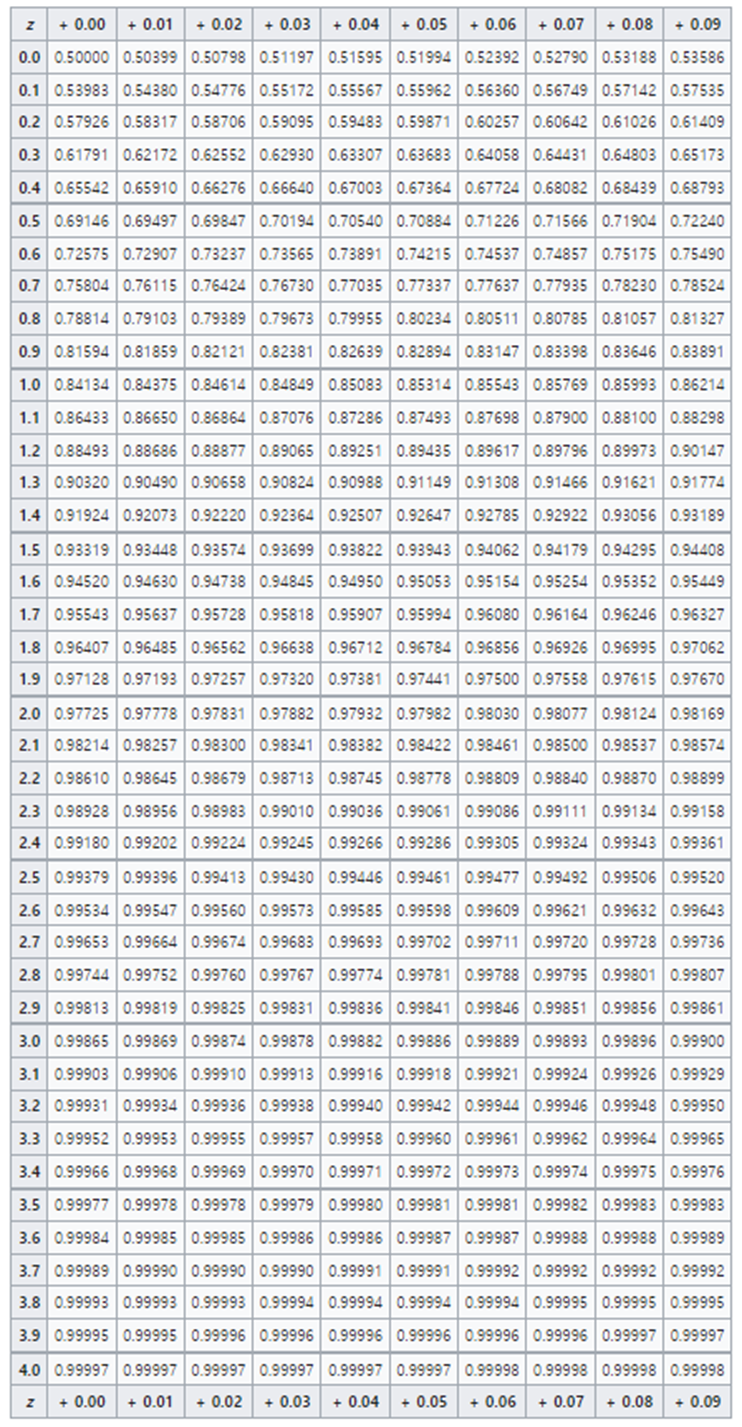
▶ 표준 정규분포의 확률계산 문제
- 그림과 0을 중심으로 대칭이라는 사실을 이용
- 표 또는 프로그램을 이용
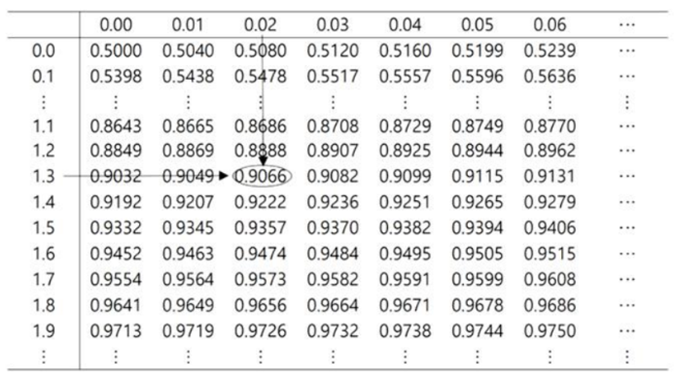
▷ Z ~ N( 0, 1 ) 이면 P (Z > 1.32 ) ?
- P (Z ≤ 1.32 ) = 0.9066
- P (Z > 1.32 ) = 1 - 0.9066 = 0.0934
▷ P(0.5 < Z <1.2 ) ?
- P(Z < 1.2 ) - P(Z<0.5 ) = 0.8849 - 0.6915 = 0.1934
▷ P (Z > 1.96 ) ?
- 1 - P( Z <1.96) = 0.975 = 0.025
▶ 표준 정규분포의 확률을 이용한 분위수 계산 문제
- α 가 주어지고 P(Z >z) = α 를 만족하는 z (분위수)를 계산

- P(Z < z ) = 0.975 를 만족시키는 z는 ? 1.96
- P(-z < Z < z ) = 0.90 을 만족시키는 z 는 ? 1.645
(3) 정규분포의 성질
▶ 정규분포의 표준화
- 확률변수 X의 평균이 μ 이고, 표준편차가 σ ( σ > 0 )인 경우
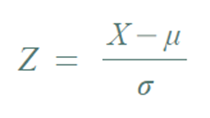
- Z : 표준화된 확률변수
- E(Z) = 0, Var(Z) = 1 ⇒ SD(Z) = 1
- 정규분포의 모수는 평균과 분산
- 모수란 함수의 특정한 성질을 나타내는 변수
▶ 선형 변환된 정규확률변수도 정규분포를 따름. ( 정규분포를 표준화해도 정규분포가 됨.)

⇒ X와 Z로 서로 변환하여 사용한다.
◈ 예제 : X ~ N(60, 16) 일때,
▶ P ( 55 ≤ X < 63 ) ?
- 표준정규분포로 표준화를 한다.

- 즉, P( -1.25 ≤ Z < 0.75 ) 로 변환할 수 있다. 표준정규분포표나 통계프로그램에서 찾아보면,
- P( Z < 0.75) = 0.7734
- P(Z < -1.25) = 0.1056
- P( -1.25 ≤ Z < 0.75 ) = 0.7734 - 0.1056 = 0.6678
▶ P(X ≤ x ) = 0.025를 만족하는 x는 ?
- 분위수를 구하는 문제
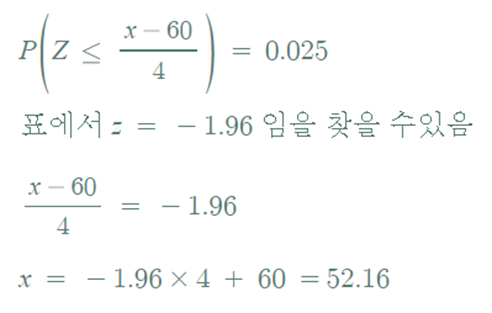
◈ 예제 : 시험점수의 분포
- 평균이 490 이고 표준편차가 50인 정규분포를 따른다면,
▷ 600점 이상 받을 확률은 ?

▷ 상위 5%인 사람의 점수는 ?

▶ 두 정규확률변수의 선형결합도 정규분포를 따름
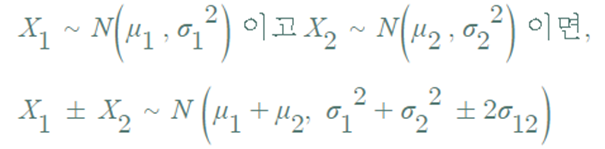
- 추가 가정 : 두 정규확률변수가 독립이면, 공분산이 0 이므로,

※ 두 정규확률변수가 정규분포를 따르고 공분산이 0이면, 두 정규확률변수는 독립이다.
( 일반적인 경우에 역은 성립하지 않으나, 정규분포에서는 역이 성립한다. )
◈ 예제 : 아침식사로 빵과 우유만 먹는다고 가정하고
- 빵의 열량 : X ~ N ( 200, 144 ) 인 정규분포를 따르고,
- 우유의 열량 : Y ~ N (85, 81)인 정규분포를 따른다고 할 때
▷ 300kcal 이상 섭취할 확률은 ?

▷동일한 식사를 일주일 했을 때, 300kcal이상 섭취할 날이 하루일 확률은 ?
- 동일한 식사를 반복하므로 매일 300kcal이상 섭취할 확률은 0.1587로 동일하다
- 이 경우 하루일 확률 X는 이항분포로 계산한다.

'통계학 공부' 카테고리의 다른 글
| 29. 표집분포, 대수의 법칙, 중심극한정리 (0) | 2023.05.11 |
|---|---|
| 28. 확률표본과 통계량 그리고 표집분포 (0) | 2023.05.10 |
| 26. 이산확률분포 - 다항분포 (Multinomial Distribution) (0) | 2023.05.08 |
| 25. 이산확률분포 - 기하분포 & 음이항분포 (0) | 2023.05.07 |
| 24. 이산확률분포 - 포아송 분포 (Poisson Distribution) (1) | 2023.05.06 |




댓글