확률분포의 분류
▷ 이산확률분포 : 베르누이 분포, 이항분포, 초기하분포, 포아송분포, 기하분포, 음이항분포, 다항분포 등
▷ 연속확률분포 : 정규분포, t 분포, 카이제곱분포, F 분포 등
(1) 다항분포 (Multinomial Distribution)
- 다항 분포는 여러 개의 값을 가질 수 있는 독립 확률변수들에 대한 확률분포로, 여러 번의 독립적 시행에서 각각의 값이 특정 횟수가 나타날 확률을 정의한다. 다항 분포에서 차원이 2인 경우 이항 분포가 된다.
- 각 시행에서 발생가능한 결과는 k 가지
- 각 시행에서 i번째 결과의 확률은 Pi로 고정
- 각 시행은 독립적을 수행
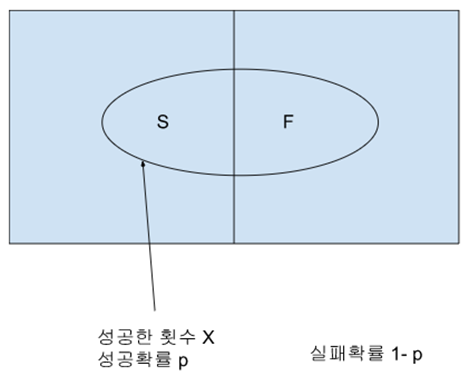
▶ 이항분포를 그림으로 표현하면,
▶ 다항분포를 그림으로 표현하면,
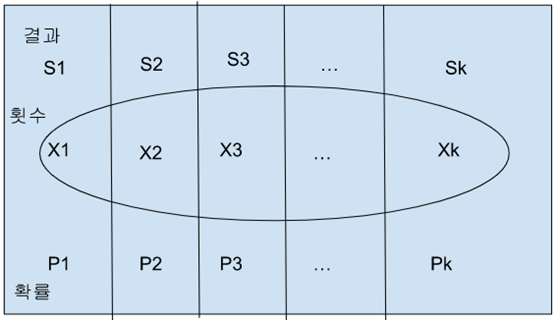
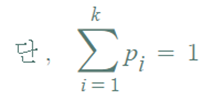
▶ n번 시행했을 때, 각 결과의 횟수를 도수분포표로 나타내면,
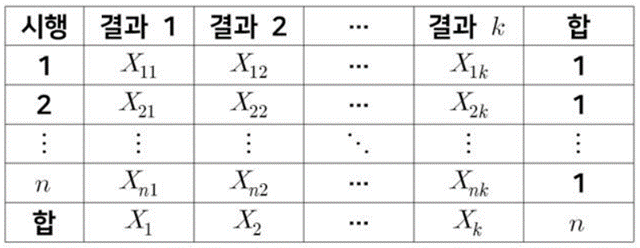

▶ 다항분포의 확률질량함수
- 각 결과값의 기준으로는 이항분포를 나타난다.
- 즉 X1 ~ B(n, p1)


위의 식을 확장하면 아래의 다항분포 확률질량함수를 구할 수 있다.
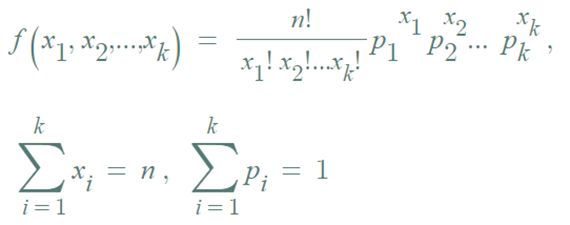
◈ 활용 : 멘델의 유전법칙
▶ 독립의 법칙 : 완두의 껍질 모양 ( R, r ), 색깔 (Y,y )
- RRYY ,rryy인 완두 교배 1대를 자기수분시킨 2대의 발현비율
- RY : Ry : rY : ry = 9 : 3 : 3 : 1
▶ 독립적으로 n개의 2 대를 얻었을 때, (RY, Ry, rY, ry)에 속한 완두의 수를 (X1, X2, X3, X4 )라고 하면,
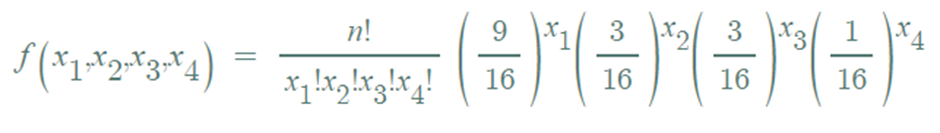
▶ 특정결과에만 관심이 있는 경우 ⇒ 이항분포로
- i 번째 결과에만 관심이 있다면, 나머지 결과를 따로 묶게 되면 이항분포가 됨.
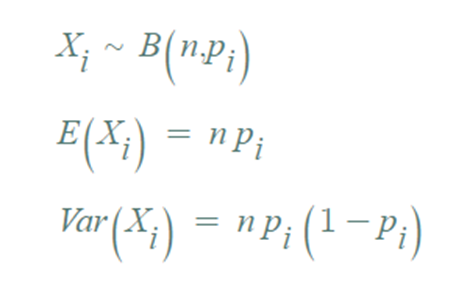
- i 번째 또는 j번째 결과에 관심이 있다면, 이는 두 합의 이항분포으로 구할 수 있다.
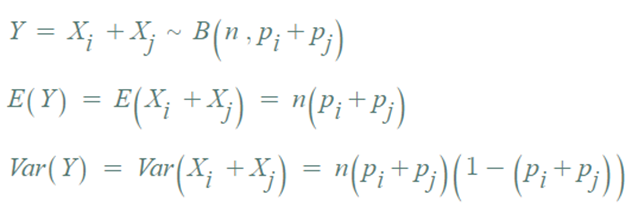
(2) 다항분포 (Multinomial Distribution)의 공분산과 상관관계
▶ Xi와 Xj 와의 관계 - 2번 실험을 하였다고 가정하면,

※ 첫번째 첨자가 다르면 즉 각 시행마다 독립이므로 11,22 와 21,12는 0 이다.
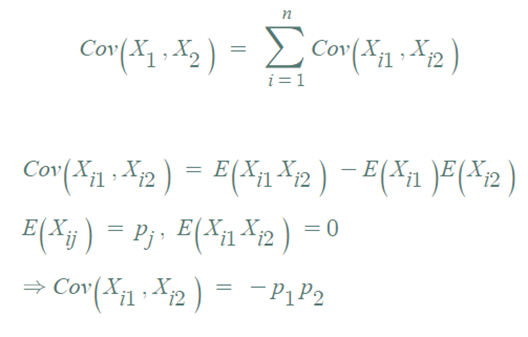
아래와 같이 공분산을 나타낼 수 있다.

▶ Var( Xi + Xj )
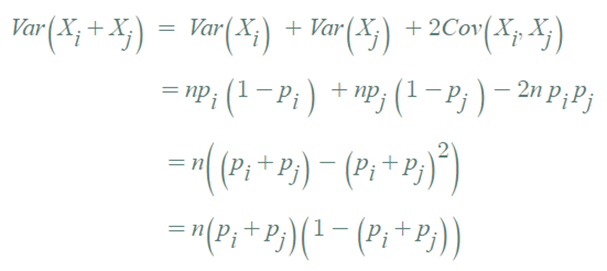
▶ Xi+Xj의 이항분포.
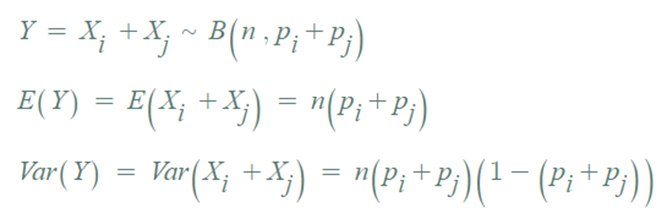
⇒ 결국 Xi+Xj의 이항분포와 동일한 결과가 나온다.
▶ 상관계수

※ 오즈 ( Odd ) : 성공할 확률이 실패할 확률의 몇 배인지 알려준다.
즉 성공 확률에서 실패할 확률을 나눈 형태이다.
위 상관계수를 따로 분리해서 보면,

상관계수는 각 결과값의 성공확률에서 실패확률을 나눈 값들의 곱이다.
◈ 활용 : 멘델의 유전법칙
▶ 독립의 법칙 : 완두의 껍질 모양 ( R, r ), 색깔 (Y,y )
- RRYY ,rryy인 완두 교배 1대를 자기수분시킨 2대의 발현비율
- RY : Ry : rY : ry = 9 : 3 : 3 : 1
▶ 껍질모양( R , r ) 에만 관심이 있는 경우
- R : r = RY+Ry : rY+ry = 12:4 = 3:1
- R의 갯수 RY(X1)+Ry(X2)~ B(n, 0.75) ( p = 12/16)
-
▶100개의 완두에 대해 우성인자만 있는 경우와 열성인자만 있는 완두 수의 상관계수는 ?
- (RY, Ry, rY, ry)에 속한 완두의 수를 (X1, X2, X3, X4 )라고 하면, Cor(X1,X4) 를 구하라는 것.
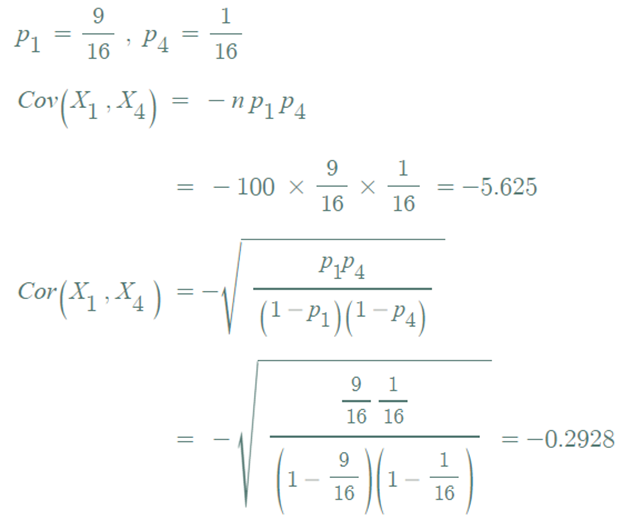
▶ X1과 X2의 상관계수 Cor(X1,X2) ?

⇒ 둘 다 큰 확률을 가지면 상대적으로 더 큰 음의 상관계수를 가진다.
'통계학 공부' 카테고리의 다른 글
| 28. 확률표본과 통계량 그리고 표집분포 (0) | 2023.05.10 |
|---|---|
| 27. 연속확률분포 - 정규분포 (Normal Distribution) (0) | 2023.05.09 |
| 25. 이산확률분포 - 기하분포 & 음이항분포 (0) | 2023.05.07 |
| 24. 이산확률분포 - 포아송 분포 (Poisson Distribution) (1) | 2023.05.06 |
| 23. 이산확률분포 - 초기하분포(Hypergeometric Distribution) (0) | 2023.05.03 |




댓글