통계학 공부 내용을 R을 이용하여 정리해 보고자 한다.
2023.04.17 - [통계학 공부] - 7. 수치 자료의 중심 - 평균, 중앙값, 최빈값
7. 수치 자료의 중심 - 평균, 중앙값, 최빈값
일변량 자료 요약 (1) 수치형 - 평균,중앙값,최빈값, 분산, 표준편차, 범위, 분위수 등 (2) 범주형 - 도수분포표 (빈도수, 백분율) 다변량 자료 요약 (1) 수치형 - 공분산, 상관관계 (2) 범주형 - 분할표
pmxsg.tistory.com
◈ 대학 정보공시 취업률 자료

(1) 자료 불러오기
Job <- scan()
55.6 83.3 43.4 58.1 31.6 55.6 60.7 64.6 73.3 55.6 64.3
52.8 22.7 46.3 71.4 53.8 64.5 67.9 71.4 80.0 59.5 40.5
77.1 58.6 65.4 52.4 66.7 91.3 41.3 72.1 61.9 78.4 63.6
41.0 65.2 81.3 54.8 19.6 50.0 53.1 41.2 56.5
(2) 중심위치
▶ 평균 : mean ( )
수치형 데이터의 평균을 구하는 함수
mean(x, na.rm = FALSE)
x: 평균을 계산할 숫자형 데이터입. 벡터, 배열, 데이터프레임 등이 가능.
na.rm: NA(결측값)를 제외하고 평균을 계산할지 여부를 나타내는 논리값.
기본값은 FALSE로, NA가 포함된 경우 평균을 NA로 반환.
TRUE로 설정하면 NA를 제외하고 평균을 계산.mean(Job)
- 표본평균의 일반식
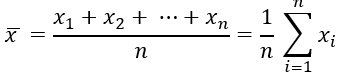
n <- length(Job)
sum(Job)/n
- length( ) : 데이터의 크기를 구하는 함수 , n = 42
- sum ( ) : 데이터의 합계를 구하는 함수 , sum(Job) = 2,468.4
▶ 가중평균 : weighted.mean ( )
수치자료에 가중치를 더해 구한 평균값이다.
weighted.mean(x, w, na.rm = FALSE)
x: 가중 평균을 계산할 숫자형 데이터. 벡터, 배열, 데이터프레임 등이 가능.
w: 각 값에 대한 가중치입니다. x와 길이가 같은 벡터로 제공되어야 한다.

◈ 투자 수익률 구하기
- 전체 투자금의 70%를 투자한 금융상품의 수익률 : 28%
- 전체 투자금의 30%를 투자한 금융상품의 수익률 : - 28%
- 이 때 전체 투자금의 수익률은 ?
x <- c(0.28,-0.28)
w <- c(700,300)
weighted.mean(x,w)
- 28%, -28%의 단순 평균은 0이지만, 가중치를 적용하였을 때의 수익률은 0.112 (11.2%) 이다.
▶ 중앙값 : median ( )
- 절반 이상의 숫자들이 이 값보다 크거나 같고 동시에 절반 이상의 숫자들이 이 값보다 작거나 같은 수이다.
- 중앙값은 n이 홀수이면 (n+1)/2번째로 크거나 작은 숫자이다
- 중앙값은 n이 짝수이면 n/2번째 숫자와 (n+1)/2번째 숫자의 평균으로 정의한다.

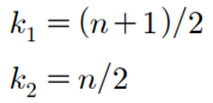
median(Job)
▶ 절사평균 : mean( x, trim)
- 표본평균은 모든 자료의 정보를 사용하지만 이상점에 로버스트 하지 않고, 표본중앙값은 로버스트 하지만 자료의 정보를 다 활용하지 못한다. 평균과 중앙점의 장점을 취합해 만든 것이 표본절사평균이다.
- a % 표본절사평균 : 순서통계량에서 하위 a %부터 상위 a%까지의 자료를 이용하여 표본평균을 계산
- a 백분위수(percentile) : 하위 a %에 해당하는 값
- p = a/100이면 p분위수(quantile)
- a를 적절히 정하면 이상점을 제외시키면서 많은 표본정보 이용
- a = 0 이면 표본평균이고, a = 50 이면 표본중앙값이다.

mean(x, trim= )
trim 매개변수는 계산에서 제외할 극단적인 값의 비율을 지정하는 값이다.
일반적으로 trim 값은 0과 0.5 사이의 값으로 지정된다.
0은 극단적인 값들을 전혀 제외하지 않음을 의미하고,
0.5는 최상위와 최하위 25%의 값들을 제외하는 것을 의미한다.- 최상위 5%와 최하위 5%의 값들을 제외
mean(Job,trim=0.1)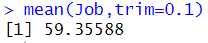
- trim = 0 이면 표본평균
mean(Job,trim=0)
- trim = 0.5 이면 표본중앙값
mean(Job,trim=0.5)
▶ 절사평균을 구하는 다른 방법
Job <- sort(Job)
trim <- c(1:3, (n-2):n)
mean(Job[-trim])- sort( ) - 오름차순으로 정렬해주는 함수
- 오름차순 정렬후 상위 3개, 하위 3개를 설정하고,
- 이 부분을 제외하고 평균을 구하는 방법
▶ 최빈값
- 자료 중 빈도가 가장 많은 값이다.
- 최빈값은 여러 개가 나올 수 있다.
- 연속자료의 경우 없을 수도 있다.
- R에서 최빈값을 바로 구하는 함수는 따로 없다.
freq <- table(Job)
maxfreq <- max(freq)
which(freq == maxfreq)
- 최빈값은 55.6 , 16번째 데이터
- table( ) 함수를 사용하여 빈도수 확인
table(Job)
- 빈도수 최대값을 찾고,
freq <- table(Job)
max(freq)
- which( ) 함수는 조건을 만족하는 요소의 인덱스를 반환하는 함수
- 이 함수를 이용하여 최빈값의 최대값의 인덱스를 찾을 수 있다.
maxfreq <- max(freq)
which(freq == maxfreq)
'R과 통계학' 카테고리의 다른 글
| 4. R을 이용한 수치자료의 산포 정리 - 분산, 표준편차,분위수 (1) | 2023.05.29 |
|---|---|
| 2. R을 이용한 자료의 요약 정리 II (0) | 2023.05.27 |
| 1. R을 이용한 자료의 요약 정리 (0) | 2023.05.18 |



댓글