통계학 공부 내용을 R을 이용해 정리해 보고자 한다.
2023.04.15 - [통계학 공부] - 5. 자료의 요약 정리
5. 자료의 요약 정리
통계학은 관심 또는 연구의 대상인 모집단의 특성을 파악하기 위해, → 모집단으로부터 일부의 자료(표본)를 수집하고 → 수집된 표본을 정리, 요약, 분석하여 표본의 특성을 파악한 후 → 표본
pmxsg.tistory.com
◈ 대학 정보공시 취업률 자료

(1) 자료 불러오기
Job <- scan()
55.6 83.3 43.4 58.1 31.6 55.6 60.7 64.6 73.3 55.6 64.3
52.8 22.7 46.3 71.4 53.8 64.5 67.9 71.4 80.0 59.5 40.5
77.1 58.6 65.4 52.4 66.7 91.3 41.3 72.1 61.9 78.4 63.6
41.0 65.2 81.3 54.8 19.6 50.0 53.1 41.2 56.5
(2) 히스토그램 (histogram) 그리기
▶ cut( ) : 연속형 변수를 구간으로 나누는 데 사용한다.
cut(x, breaks, labels = NULL, include.lowest = FALSE, right = TRUE,
dig.lab = 3, ordered_result = FALSE)
x: 나눌 연속형 변수
breaks: 구간을 나누는 기준값.
labels: 구간에 대한 레이블을 지정. 기본값은 NULL, 구간의 범위가 레이블로 사용.
include.lowest: 첫 번째 구간의 하한값을 포함할지 여부를 결정. 기본값은 FALSE
첫 번째 구간의 하한값은 포함되지 않는다.
right: 우측 경계값을 포함할지 여부를 결정. 기본값은 TRUE로, 우측 경계값을 포함한다.
dig.lab: 레이블을 소수점 몇 자리까지 표시할지 결정. 기본값은 3으로, 세 자리까지 표시.
ordered_result: 반환되는 결과를 순서형(factor) 변수로 설정할지 여부를 결정.
기본값은 FALSE로, 반환되는 결과는 범주형(factor) 변수.- 구간을 초과, 이하로 설정 ( , ]
JobCut <- cut(Job, breaks=c(10, 39.9, 49.9, 59.9, 69.9, 79.9, 100))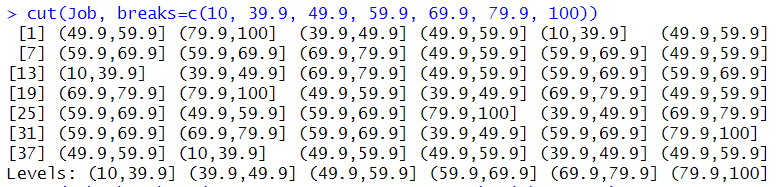
- 구간을 이상, 미만으로 설정 [ , )
cut(Job, breaks=c(10, 40, 50, 60, 70, 80, 100),right=FALSE)
- 도수분포표
JobCut <- cut(Job, breaks=c(10, 40, 50, 60, 70, 80, 100),right=FALSE)
table(JobCut)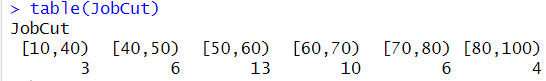
- 도수분포표 - 비율로 표시
JobFreq <- table(JobCut)
round(JobFreq/sum(JobFreq),3)
▶ cumsum( ) : 누적 합을 계산 하는데 사용 (cumulative sum)
JobProp <- round(JobFreq/sum(JobFreq),3)
cumsum(JobProp)
- 도수분포표 - 빈도수,상대도수,누적상대도수
JobFreq <- table(JobCut)
JobProp <- round(JobFreq/sum(JobFreq),3)
CumJobProp <- cumsum(JobProp)
cbind(JobFreq,JobProp,CumJobProp)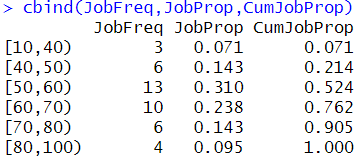
▶ colname( ) : 컬럼 이름을 설정한다.
▶ rowname( ) : 행 이름을 설정한다.
Result <- cbind(JobFreq,JobProp,CumJobProp)
colnames(Result) <- c("학과수","상대도수","누적상대도수")
rownames(Result) <- c("10%이상~40%미만","40%이상~50%미만","50%이상~60%미만",
"60%이상~70%미만","70%이상~80%미만","80%이상~100%")
Result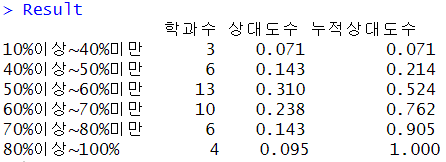
▶ hist( ) : 히스토그램을 생성하는 함수
hist(x, breaks = "", col = "", main = "", xlab = "", ylab = "", ...)
x: 히스토그램을 생성할 데이터 벡터 또는 수치형 변수
breaks: 히스토그램의 구간(bin) 개수를 지정
col: 히스토그램의 막대 색상을 지정.
main: 히스토그램의 제목을 지정.
xlab: x축의 레이블을 지정.
ylab: y축의 레이블을 지정.hist(Job)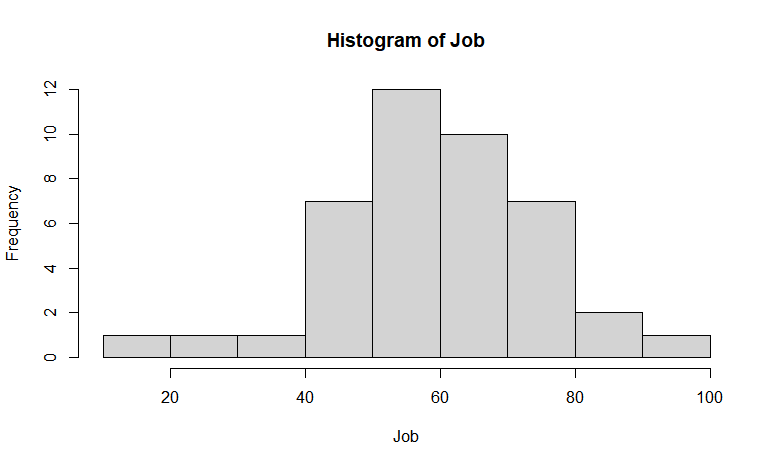
▶ hist() 함수에서 freq와 probability는 히스토그램 막대의 높이를 조정하는 매개변수.
- freq: 기본값은 TRUE. 이 경우, 히스토그램의 막대 높이는 해당 구간(bin)에 속하는 데이터의 빈도수로 표시. 즉, 막대 높이는 해당 구간 내에 포함된 데이터의 개수이다.
- probability: 히스토그램의 막대 높이는 해당 구간에 속하는 데이터의 상대적인 비율 또는 확률로 표시된다. 즉, 막대 높이는 해당 구간 내의 데이터 비율 또는 확률이다. probability를 TRUE로 설정하면 히스토그램의 총 면적이 1이 되도록 조정된다.
hist(Job,freq=FALSE)hist(Job, probability=TRUE)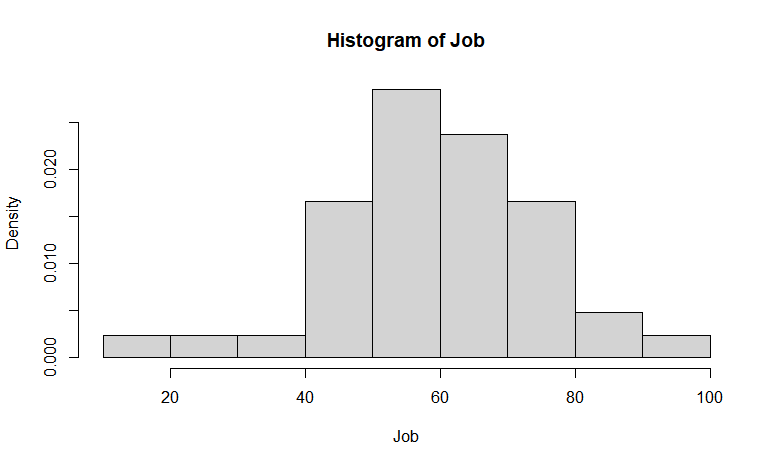
par(mfrow=c(1,2))
hist(Job,freq=FALSE,ylim=c(0,0.035)) # hist(Job, probability=TRUE)
hist(Job,breaks = c(10, 39.99, 49.99, 59.99, 69.99, 79.99, 100),
main = "취업률 히스토그램", xlab = "취업률", ylab = "밀도",ylim=c(0,0.035), col="steelblue")
(3) 줄기-잎 그림 (stem-and-leaf plot)
stem(Job)
◈ 학점자료
- 도수분포표
score<-read.table("score.txt")
table(score)
- 도수분포표 - 빈도수,상대도수,누적상대도수
scoreFreq<-table(score)
scoreProp<-round(scoreFreq/sum(scoreFreq),3)
CumscoreProp<-cumsum(scoreProp)
Result2<-cbind(scoreFreq,scoreProp,CumscoreProp)
colnames(Result2) <- c("학생수","상대도수","누적상대도수")
Result2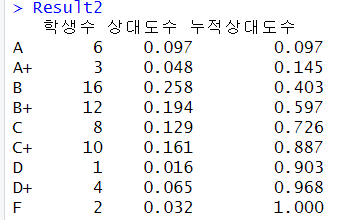
- 막대그래프
par(mfrow=c(1,2))
barplot(scoreFreq,main="도수비교 막대그래프",col="blue")
abline(h=0)
barplot(scoreProp,main="상대도수비교 막대그래프",col="orange")
abline(h=0)
'R과 통계학' 카테고리의 다른 글
| 4. R을 이용한 수치자료의 산포 정리 - 분산, 표준편차,분위수 (1) | 2023.05.29 |
|---|---|
| 3. R을 이용한 수치자료의 중심 정리 - 평균,중앙값,최빈값 (1) | 2023.05.28 |
| 1. R을 이용한 자료의 요약 정리 (0) | 2023.05.18 |



댓글